
Concept explainers
Rutherford’s Experiment In May 1911, Ernest Rutherford published a paper in Philosophical Magazine. In this article, he described the motion of alpha particles as they are shot at a piece of gold foil 0.00004 cm thick. Before conducting this experiment, Rutherford expected that the alpha particles would shoot through the foil just as a bullet would shoot through snow. Instead, a small fraction of the alpha particles bounced off the foil. This led to the conclusion that the nucleus of an atom is dense, while the remainder of the atom is sparse. Only the density of the nucleus could cause the alpha particles to deviate from their path. The figure shows a diagram from Rutherford’s paper that indicates that the deflected alpha particles follow the path of one branch of a hyperbola.
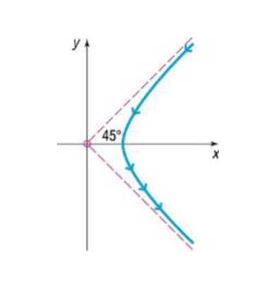
(a) Find an equation of the asymptotes under this scenario.
(b) If the vertex of the path of the alpha particles is 10 cm from the center of the hyperbola, find a model that describes the path of the particle.
Want to see the full answer?
Check out a sample textbook solution
Chapter 10 Solutions
Precalculus (10th Edition)
Additional Math Textbook Solutions
Elementary Statistics: Picturing the World (7th Edition)
Basic Business Statistics, Student Value Edition
Intro Stats, Books a la Carte Edition (5th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
University Calculus: Early Transcendentals (4th Edition)
Algebra and Trigonometry (6th Edition)
- please solve with full steps pleasearrow_forward4. Identify at least two mistakes in Francisco's work. Correct the mistakes and complete the problem by using the second derivative test. 2f 2X 2. Find the relative maximum and relative minimum points of f(x) = 2x3 + 3x² - 3, using the First Derivative Test or the Second Derivative Test. bx+ bx 6x +6x=0 12x- af 24 = 0 x=0 108 -2 5. Identify at least three mistakes in Francisco's work. Then sketch the graph of the function and label the local max and local min. 1. Find the equation of the tangent line to the curve y=x-2x3+x-2 at the point (1.-2). Sketch the araph of y=x42x3+x-2 and the tangent line at (1,-2) y' = 4x-6x y' (1) = 4(1) - 667 - 2 = 4(-2)4127-6(-2) 5-8-19-20 =arrow_forward۳/۱ R2X2 2) slots per pole per phase = 3/31 B=18060 msl Ka, Sin (1) Kdl Isin ( sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 120*50 5) Synchronous speed, 120 x 50 S1000-950 1000 Copper losses 5kw 50105 Rotor input 5 0.05 loo kw 6) 1 1000rpm اذا ميريد شرح الكتب فقط Look = 7) rotov DC ined sove in peaper PU + 96er Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. 3" 6" Σ=1 (2-1) π X9arrow_forward
- 1 R2 X2 2) slots per pole per phase = 3/31 B = 180 - 60 msl Kd Kol, Sin (no) Isin (6) 2 sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed; 120*50 Looo rem G S = 1000-950 solos 1000 Copper losses: 5kw Rotor input: 5 loo kw 0.05 1 اذا میرید شرح الكتب فقط look 7) rotor DC ined sove in pea PU+96er Q2// Find the volume of the solid bounded above by the cynnuer 2=6-x², on the sides by the cylinder x² + y² = 9, and below by the xy-plane. Q041 Convert 2 2x-2 Lake Gex 35 w2x-xབོ ,4-ཙཱཔ-y √4-x²-yz 21xy²dzdydx to(a) cylindrical coordinates, (b) Spherical coordinates. 201 25arrow_forwardshow full work pleasearrow_forward3. Describe the steps you would take to find the absolute max of the following function using Calculus f(x) = : , [-1,2]. Then use a graphing calculator to x-1 x²-x+1 approximate the absolute max in the closed interval.arrow_forward
- (7) (12 points) Let F(x, y, z) = (y, x+z cos yz, y cos yz). Ꮖ (a) (4 points) Show that V x F = 0. (b) (4 points) Find a potential f for the vector field F. (c) (4 points) Let S be a surface in R3 for which the Stokes' Theorem is valid. Use Stokes' Theorem to calculate the line integral Jos F.ds; as denotes the boundary of S. Explain your answer.arrow_forward(3) (16 points) Consider z = uv, u = x+y, v=x-y. (a) (4 points) Express z in the form z = fog where g: R² R² and f: R² → R. (b) (4 points) Use the chain rule to calculate Vz = (2, 2). Show all intermediate steps otherwise no credit. (c) (4 points) Let S be the surface parametrized by T(x, y) = (x, y, ƒ (g(x, y)) (x, y) = R². Give a parametric description of the tangent plane to S at the point p = T(x, y). (d) (4 points) Calculate the second Taylor polynomial Q(x, y) (i.e. the quadratic approximation) of F = (fog) at a point (a, b). Verify that Q(x,y) F(a+x,b+y). =arrow_forward(6) (8 points) Change the order of integration and evaluate (z +4ry)drdy . So S√ ² 0arrow_forward
- (10) (16 points) Let R>0. Consider the truncated sphere S given as x² + y² + (z = √15R)² = R², z ≥0. where F(x, y, z) = −yi + xj . (a) (8 points) Consider the vector field V (x, y, z) = (▼ × F)(x, y, z) Think of S as a hot-air balloon where the vector field V is the velocity vector field measuring the hot gasses escaping through the porous surface S. The flux of V across S gives the volume flow rate of the gasses through S. Calculate this flux. Hint: Parametrize the boundary OS. Then use Stokes' Theorem. (b) (8 points) Calculate the surface area of the balloon. To calculate the surface area, do the following: Translate the balloon surface S by the vector (-15)k. The translated surface, call it S+ is part of the sphere x² + y²+z² = R². Why do S and S+ have the same area? ⚫ Calculate the area of S+. What is the natural spherical parametrization of S+?arrow_forward(1) (8 points) Let c(t) = (et, et sint, et cost). Reparametrize c as a unit speed curve starting from the point (1,0,1).arrow_forward(9) (16 points) Let F(x, y, z) = (x² + y − 4)i + 3xyj + (2x2 +z²)k = - = (x²+y4,3xy, 2x2 + 2²). (a) (4 points) Calculate the divergence and curl of F. (b) (6 points) Find the flux of V x F across the surface S given by x² + y²+2² = 16, z ≥ 0. (c) (6 points) Find the flux of F across the boundary of the unit cube E = [0,1] × [0,1] x [0,1].arrow_forward
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
