CALCULUS
11th Edition
ISBN: 9781337761512
Author: Larson
Publisher: CENGAGE L
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 10.3, Problem 85E
Areas of Simple Closed Curves In Exercises 81-86, use a computer algebra system and the result of Exercise 77 to match the closed curse with its area. (These exercises were based on “The Surveyor’s Area Formula'’ by Bart Braden, College Mathematics Journal, September 1986, pp. 335-337, by permission of the author.)
(a)
(b)
(c)
(d)
(e)
(f)
Hourglass:
Expert Solution & Answer
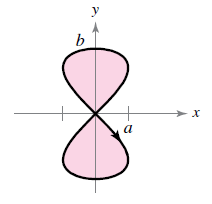
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Find the equation of the line / in the figure below. Give exact values using the form y = mx + b.
m =
b =
y
WebAssign Plot
f(x) = 10*
log 9
X
A particle travels along a straight line path given by s=9.5t3-2.2t2-4.5t+9.9 (in meters).
What time does it change direction?
Report the higher of the answers to the nearest 2 decimal places in seconds.
Use the method of disks to find the volume of the solid that is obtained
when the region under the curve y = over the interval [4,17] is rotated
about the x-axis.
Chapter 10 Solutions
CALCULUS
Ch. 10.1 - Conic Sections State the definitions of parabola,...Ch. 10.1 - Prob. 2ECh. 10.1 - Prob. 3ECh. 10.1 - Prob. 4ECh. 10.1 - Matching In Exercises 5-10, match the equation...Ch. 10.1 - Matching In Exercises 5-10, match the equation...Ch. 10.1 - Matching In Exercises 5-10, match the equation...Ch. 10.1 - Matching In Exercises 5-10, match the equation...Ch. 10.1 - Matching In Exercises 5-10, match the equation...Ch. 10.1 - Prob. 10E
Ch. 10.1 - Prob. 11ECh. 10.1 - Sketching a Parabola In Exercises 1116, find the...Ch. 10.1 - Sketching a Parabola In Exercises 1116, find the...Ch. 10.1 - Prob. 14ECh. 10.1 - Prob. 15ECh. 10.1 - Prob. 16ECh. 10.1 - Prob. 17ECh. 10.1 - Prob. 18ECh. 10.1 - Prob. 19ECh. 10.1 - Prob. 20ECh. 10.1 - Prob. 21ECh. 10.1 - Prob. 22ECh. 10.1 - Prob. 23ECh. 10.1 - Prob. 24ECh. 10.1 - Prob. 25ECh. 10.1 - Prob. 26ECh. 10.1 - Prob. 27ECh. 10.1 - Prob. 28ECh. 10.1 - Prob. 29ECh. 10.1 - Prob. 30ECh. 10.1 - Prob. 31ECh. 10.1 - Prob. 32ECh. 10.1 - Prob. 33ECh. 10.1 - Prob. 34ECh. 10.1 - Prob. 35ECh. 10.1 - Finding the Standard Equation of an Ellipse In...Ch. 10.1 - Prob. 37ECh. 10.1 - Prob. 38ECh. 10.1 - Prob. 39ECh. 10.1 - Prob. 40ECh. 10.1 - Prob. 41ECh. 10.1 - Prob. 42ECh. 10.1 - Prob. 43ECh. 10.1 - Prob. 44ECh. 10.1 - Prob. 45ECh. 10.1 - Prob. 46ECh. 10.1 - Prob. 47ECh. 10.1 - Prob. 48ECh. 10.1 - Prob. 49ECh. 10.1 - Prob. 50ECh. 10.1 - Prob. 51ECh. 10.1 - Prob. 52ECh. 10.1 - Prob. 53ECh. 10.1 - Classifying the Graph of an Equation In Exercises...Ch. 10.1 - Prob. 55ECh. 10.1 - Prob. 56ECh. 10.1 - Prob. 57ECh. 10.1 - Prob. 58ECh. 10.1 - Prob. 59ECh. 10.1 - Prob. 60ECh. 10.1 - Solar Collector A solar collector for heating...Ch. 10.1 - Beam Deflection A simply supported beam that is 16...Ch. 10.1 - Prob. 63ECh. 10.1 - Proof (a) Prove that if any two tangent lines to a...Ch. 10.1 - Bridge Design A cable of a suspension bridge is...Ch. 10.1 - Arc Length Find the length of the parabolic cable...Ch. 10.1 - Prob. 67ECh. 10.1 - Surface Area A satellite signal receiving dish is...Ch. 10.1 - Prob. 69ECh. 10.1 - Prob. 70ECh. 10.1 - Prob. 71ECh. 10.1 - Prob. 72ECh. 10.1 - Prob. 73ECh. 10.1 - Prob. 74ECh. 10.1 - Prob. 75ECh. 10.1 - Prob. 76ECh. 10.1 - Prob. 77ECh. 10.1 - Conjecture Show that the equation of an ellipse...Ch. 10.1 - Prob. 79ECh. 10.1 - Prob. 80ECh. 10.1 - Prob. 81ECh. 10.1 - Prob. 82ECh. 10.1 - Prob. 83ECh. 10.1 - Hyperbolic Mirror A hyperbolic mirror (used in...Ch. 10.1 - Prob. 85ECh. 10.1 - Prob. 86ECh. 10.1 - True or False? In Exercises 8792, determine...Ch. 10.1 - Prob. 88ECh. 10.1 - True or False? In Exercises 87-92, determine...Ch. 10.1 - True or False? In Exercises 87-92, determine...Ch. 10.1 - True or False? In Exercises 8792, determine...Ch. 10.1 - Prob. 92ECh. 10.1 - For a point P on an ellipse, let d be the distance...Ch. 10.1 - Prob. 94ECh. 10.2 - Parametric Equations What information does a set...Ch. 10.2 - Prob. 2ECh. 10.2 - Prob. 3ECh. 10.2 - Prob. 4ECh. 10.2 - Prob. 5ECh. 10.2 - Prob. 6ECh. 10.2 - Prob. 7ECh. 10.2 - Prob. 8ECh. 10.2 - Prob. 9ECh. 10.2 - Prob. 10ECh. 10.2 - Prob. 11ECh. 10.2 - Prob. 12ECh. 10.2 - Prob. 13ECh. 10.2 - Prob. 14ECh. 10.2 - Prob. 15ECh. 10.2 - Prob. 16ECh. 10.2 - Prob. 17ECh. 10.2 - Prob. 18ECh. 10.2 - Using Parametric Equations In Exercises 5-22,...Ch. 10.2 - Using Parametric Equations In Exercises 5-22,...Ch. 10.2 - Prob. 21ECh. 10.2 - Using Parametric Equations In Exercises 5-22,...Ch. 10.2 - Using Parametric Equations In Exercises 23-34, use...Ch. 10.2 - Using Parametric Equations In Exercises 23-34, use...Ch. 10.2 - Prob. 25ECh. 10.2 - Prob. 26ECh. 10.2 - Prob. 27ECh. 10.2 - Prob. 28ECh. 10.2 - Using Parametric Equations In Exercises 23-34, use...Ch. 10.2 - Prob. 30ECh. 10.2 - Using Parametric Equations In Exercises 23-34, use...Ch. 10.2 - Using Parametric Equations In Exercises 23-34, use...Ch. 10.2 - Prob. 33ECh. 10.2 - Prob. 34ECh. 10.2 - Prob. 35ECh. 10.2 - Prob. 36ECh. 10.2 - Prob. 37ECh. 10.2 - Prob. 38ECh. 10.2 - Prob. 39ECh. 10.2 - Prob. 40ECh. 10.2 - Prob. 41ECh. 10.2 - Prob. 42ECh. 10.2 - Writing a Set of Parametric Equations In Exercises...Ch. 10.2 - Prob. 44ECh. 10.2 - Writing a Set of Parametric Equations In Exercises...Ch. 10.2 - Prob. 46ECh. 10.2 - Writing a Set of Parametric Equations In Exercises...Ch. 10.2 - Writing a Set of Parametric Equations In Exercises...Ch. 10.2 - Writing a Set of Parametric Equations In Exercises...Ch. 10.2 - Writing a Set of Parametric Equations In Exercises...Ch. 10.2 - Prob. 51ECh. 10.2 - Prob. 52ECh. 10.2 - Prob. 53ECh. 10.2 - Prob. 54ECh. 10.2 - Prob. 55ECh. 10.2 - Prob. 56ECh. 10.2 - Prob. 57ECh. 10.2 - Prob. 58ECh. 10.2 - Prob. 59ECh. 10.2 - Prob. 60ECh. 10.2 - Prob. 61ECh. 10.2 - Prob. 62ECh. 10.2 - Prob. 63ECh. 10.2 - Prob. 64ECh. 10.2 - Prob. 65ECh. 10.2 - Prob. 66ECh. 10.2 - Orientation Describe the orientation of the...Ch. 10.2 - Prob. 68ECh. 10.2 - Prob. 69ECh. 10.2 - Prob. 70ECh. 10.2 - Prob. 71ECh. 10.2 - Prob. 72ECh. 10.2 - Prob. 73ECh. 10.2 - Prob. 74ECh. 10.2 - Prob. 75ECh. 10.2 - Epicycloid A circle of radius 1 rolls around the...Ch. 10.2 - Prob. 77ECh. 10.2 - Prob. 78ECh. 10.2 - Prob. 79ECh. 10.2 - Prob. 80ECh. 10.2 - Projectile Motion In Exercises 81 and 82, consider...Ch. 10.2 - Projectile Motion In Exercises 81 and 82, consider...Ch. 10.3 - Parametric Form of the Derivative What does the...Ch. 10.3 - Prob. 2ECh. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Prob. 7ECh. 10.3 - Prob. 8ECh. 10.3 - Prob. 9ECh. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Prob. 12ECh. 10.3 - Prob. 13ECh. 10.3 - Prob. 14ECh. 10.3 - Prob. 15ECh. 10.3 - Prob. 16ECh. 10.3 - Prob. 17ECh. 10.3 - Prob. 18ECh. 10.3 - Prob. 19ECh. 10.3 - Prob. 20ECh. 10.3 - Prob. 21ECh. 10.3 - Prob. 22ECh. 10.3 - Prob. 23ECh. 10.3 - Prob. 24ECh. 10.3 - Finding an Equation of a Tangent Line In Exercises...Ch. 10.3 - Prob. 26ECh. 10.3 - Prob. 27ECh. 10.3 - Finding Equations of Tangent Lines In Exercises...Ch. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - Prob. 31ECh. 10.3 - Horizontal and Vertical Tangency In Exercises 31...Ch. 10.3 - Prob. 33ECh. 10.3 - Prob. 34ECh. 10.3 - Prob. 35ECh. 10.3 - Prob. 36ECh. 10.3 - Prob. 37ECh. 10.3 - Prob. 38ECh. 10.3 - Prob. 39ECh. 10.3 - Prob. 40ECh. 10.3 - Prob. 41ECh. 10.3 - Prob. 42ECh. 10.3 - Prob. 43ECh. 10.3 - Prob. 44ECh. 10.3 - Prob. 45ECh. 10.3 - Prob. 46ECh. 10.3 - Prob. 47ECh. 10.3 - Prob. 48ECh. 10.3 - Prob. 49ECh. 10.3 - Prob. 50ECh. 10.3 - Prob. 51ECh. 10.3 - Prob. 52ECh. 10.3 - Arc Length In Exercises 49-54, find the arc length...Ch. 10.3 - Arc Length In Exercises 49-54, find the arc length...Ch. 10.3 - Arc Length In Exercises 55-58, find the arc length...Ch. 10.3 - Arc Length In Exercises 55-58, find the arc length...Ch. 10.3 - Prob. 57ECh. 10.3 - Prob. 58ECh. 10.3 - Prob. 59ECh. 10.3 - Prob. 60ECh. 10.3 - Prob. 61ECh. 10.3 - Prob. 62ECh. 10.3 - Surface Area In Exercises 63-68, find the area of...Ch. 10.3 - Prob. 64ECh. 10.3 - Surface Area In Exercises 63-68, find the area of...Ch. 10.3 - Prob. 66ECh. 10.3 - Prob. 67ECh. 10.3 - Prob. 68ECh. 10.3 - Prob. 69ECh. 10.3 - Surface Area In Exercises 69-72, write an integral...Ch. 10.3 - Prob. 71ECh. 10.3 - Prob. 72ECh. 10.3 - Prob. 73ECh. 10.3 - Prob. 74ECh. 10.3 - Prob. 75ECh. 10.3 - Prob. 76ECh. 10.3 - Prob. 77ECh. 10.3 - Prob. 78ECh. 10.3 - Area In Exercises 79 and 80, find the area of the...Ch. 10.3 - Prob. 80ECh. 10.3 - Prob. 81ECh. 10.3 - Prob. 82ECh. 10.3 - Prob. 83ECh. 10.3 - Prob. 84ECh. 10.3 - Areas of Simple Closed Curves In Exercises 81-86,...Ch. 10.3 - Prob. 86ECh. 10.3 - Prob. 87ECh. 10.3 - Prob. 88ECh. 10.3 - Prob. 89ECh. 10.3 - Volume In Exercises 89 and 90, find the volume of...Ch. 10.3 - Prob. 91ECh. 10.3 - Prob. 92ECh. 10.3 - Prob. 93ECh. 10.3 - Prob. 94ECh. 10.3 - Prob. 95ECh. 10.3 - Prob. 96ECh. 10.3 - True or False? In Exercises 97-100, determine...Ch. 10.3 - Prob. 98ECh. 10.3 - Prob. 99ECh. 10.3 - True or False ? In Exercises 97-100, determine...Ch. 10.4 - Polar Coordinates Consider the polar coordinates...Ch. 10.4 - Prob. 2ECh. 10.4 - Prob. 3ECh. 10.4 - Prob. 4ECh. 10.4 - Prob. 5ECh. 10.4 - Prob. 6ECh. 10.4 - Prob. 7ECh. 10.4 - Prob. 8ECh. 10.4 - Prob. 9ECh. 10.4 - Prob. 10ECh. 10.4 - Prob. 11ECh. 10.4 - Prob. 12ECh. 10.4 - Prob. 13ECh. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Prob. 17ECh. 10.4 - Prob. 18ECh. 10.4 - Prob. 19ECh. 10.4 - Prob. 20ECh. 10.4 - Prob. 21ECh. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Prob. 24ECh. 10.4 - Prob. 25ECh. 10.4 - Prob. 26ECh. 10.4 - Rectangular-to Polar Conversion In Exercises 2534,...Ch. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.4 - Prob. 30ECh. 10.4 - Prob. 31ECh. 10.4 - Prob. 32ECh. 10.4 - Prob. 33ECh. 10.4 - Rectangular-to-Polar Conversion In Exercises...Ch. 10.4 - Prob. 35ECh. 10.4 - Prob. 36ECh. 10.4 - Prob. 37ECh. 10.4 - Prob. 38ECh. 10.4 - Prob. 39ECh. 10.4 - Prob. 40ECh. 10.4 - Prob. 41ECh. 10.4 - Prob. 42ECh. 10.4 - Prob. 43ECh. 10.4 - Polar-to-Rectangular Conversion In Exercises...Ch. 10.4 - Prob. 45ECh. 10.4 - Prob. 46ECh. 10.4 - Prob. 47ECh. 10.4 - Prob. 48ECh. 10.4 - Prob. 49ECh. 10.4 - Prob. 50ECh. 10.4 - Prob. 51ECh. 10.4 - Prob. 52ECh. 10.4 - Prob. 53ECh. 10.4 - Prob. 54ECh. 10.4 - Prob. 55ECh. 10.4 - Prob. 56ECh. 10.4 - Prob. 57ECh. 10.4 - Prob. 58ECh. 10.4 - Prob. 59ECh. 10.4 - Prob. 60ECh. 10.4 - Prob. 61ECh. 10.4 - Prob. 62ECh. 10.4 - Prob. 63ECh. 10.4 - Prob. 64ECh. 10.4 - Prob. 65ECh. 10.4 - Prob. 66ECh. 10.4 - Prob. 67ECh. 10.4 - Prob. 68ECh. 10.4 - Prob. 69ECh. 10.4 - Prob. 70ECh. 10.4 - Prob. 71ECh. 10.4 - Prob. 72ECh. 10.4 - Prob. 73ECh. 10.4 - Prob. 74ECh. 10.4 - Prob. 75ECh. 10.4 - Prob. 76ECh. 10.4 - Prob. 77ECh. 10.4 - Prob. 78ECh. 10.4 - Prob. 79ECh. 10.4 - Prob. 80ECh. 10.4 - Prob. 81ECh. 10.4 - Prob. 82ECh. 10.4 - Prob. 83ECh. 10.4 - Prob. 84ECh. 10.4 - Prob. 85ECh. 10.4 - Prob. 86ECh. 10.4 - Prob. 87ECh. 10.4 - Prob. 88ECh. 10.4 - Prob. 89ECh. 10.4 - Prob. 90ECh. 10.4 - Prob. 91ECh. 10.4 - Prob. 92ECh. 10.4 - Prob. 93ECh. 10.4 - Prob. 94ECh. 10.4 - Prob. 95ECh. 10.4 - Prob. 96ECh. 10.4 - Prob. 97ECh. 10.4 - Prob. 98ECh. 10.4 - Prob. 99ECh. 10.4 - Prob. 100ECh. 10.4 - Prob. 101ECh. 10.4 - Prob. 102ECh. 10.4 - Prob. 103ECh. 10.4 - Rotated Curve In Exercises 103-105, use the...Ch. 10.4 - Prob. 105ECh. 10.4 - Proof Prove that the tangent of the angle (0/2)...Ch. 10.4 - Prob. 107ECh. 10.4 - Prob. 108ECh. 10.4 - Prob. 109ECh. 10.4 - Prob. 110ECh. 10.4 - Prob. 111ECh. 10.4 - Prob. 112ECh. 10.4 - Prob. 113ECh. 10.4 - Prob. 114ECh. 10.4 - Prob. 115ECh. 10.4 - Prob. 116ECh. 10.5 - Area of a Polar Region What should you check...Ch. 10.5 - Points of Intersection Explain why finding points...Ch. 10.5 - Area of a Polar Region In Exercises 3-6, write an...Ch. 10.5 - Area of a Polar Region In Exercises 3-6, write an...Ch. 10.5 - Prob. 5ECh. 10.5 - Prob. 6ECh. 10.5 - Finding the Area of a Polar Region In Exercises...Ch. 10.5 - Prob. 8ECh. 10.5 - Finding the Area of a Polar Region In Exercises...Ch. 10.5 - Prob. 10ECh. 10.5 - Prob. 11ECh. 10.5 - Finding the Area of a Polar Region In Exercises...Ch. 10.5 - Prob. 13ECh. 10.5 - Prob. 14ECh. 10.5 - Prob. 15ECh. 10.5 - Prob. 16ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Prob. 20ECh. 10.5 - Prob. 21ECh. 10.5 - Prob. 22ECh. 10.5 - Prob. 23ECh. 10.5 - Prob. 24ECh. 10.5 - Prob. 25ECh. 10.5 - Prob. 26ECh. 10.5 - Prob. 27ECh. 10.5 - Finding Points of Intersection In Exercises 27-34,...Ch. 10.5 - Prob. 29ECh. 10.5 - Prob. 30ECh. 10.5 - Prob. 31ECh. 10.5 - Prob. 32ECh. 10.5 - Finding Points of Intersection In Exercises 27-34,...Ch. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - Prob. 37ECh. 10.5 - Prob. 38ECh. 10.5 - Prob. 39ECh. 10.5 - Finding the Area of a Polar Region Between Two...Ch. 10.5 - Prob. 41ECh. 10.5 - Prob. 42ECh. 10.5 - Prob. 43ECh. 10.5 - Prob. 44ECh. 10.5 - Prob. 45ECh. 10.5 - Prob. 46ECh. 10.5 - Prob. 47ECh. 10.5 - Finding the Area of a Polar Region Between Two...Ch. 10.5 - Prob. 49ECh. 10.5 - Prob. 50ECh. 10.5 - Prob. 51ECh. 10.5 - Prob. 52ECh. 10.5 - Prob. 53ECh. 10.5 - Prob. 54ECh. 10.5 - Prob. 55ECh. 10.5 - Prob. 56ECh. 10.5 - Prob. 57ECh. 10.5 - Prob. 58ECh. 10.5 - Prob. 59ECh. 10.5 - Prob. 60ECh. 10.5 - Prob. 61ECh. 10.5 - Prob. 62ECh. 10.5 - Prob. 63ECh. 10.5 - Prob. 64ECh. 10.5 - Prob. 65ECh. 10.5 - Prob. 66ECh. 10.5 - Prob. 67ECh. 10.5 - Prob. 68ECh. 10.5 - Prob. 69ECh. 10.5 - Prob. 70ECh. 10.5 - Prob. 71ECh. 10.5 - Prob. 72ECh. 10.5 - Prob. 73ECh. 10.5 - Prob. 74ECh. 10.5 - Surface Area of a Torus Find the surface area of...Ch. 10.5 - Surface Area of a Tours Find the surface area of...Ch. 10.5 - Prob. 77ECh. 10.5 - Prob. 78ECh. 10.5 - Prob. 79ECh. 10.5 - Logarithmic Spiral The curve represented by the...Ch. 10.5 - Prob. 81ECh. 10.5 - Prob. 82ECh. 10.5 - Prob. 83ECh. 10.5 - Prob. 84ECh. 10.6 - Prob. 1ECh. 10.6 - Prob. 2ECh. 10.6 - Prob. 3ECh. 10.6 - Prob. 4ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Prob. 7ECh. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - Prob. 11ECh. 10.6 - Prob. 12ECh. 10.6 - Prob. 13ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - Prob. 16ECh. 10.6 - Prob. 17ECh. 10.6 - Prob. 18ECh. 10.6 - Prob. 19ECh. 10.6 - Prob. 20ECh. 10.6 - Prob. 21ECh. 10.6 - Prob. 22ECh. 10.6 - Prob. 23ECh. 10.6 - Prob. 24ECh. 10.6 - Prob. 25ECh. 10.6 - Prob. 26ECh. 10.6 - Prob. 27ECh. 10.6 - Prob. 28ECh. 10.6 - Prob. 29ECh. 10.6 - Prob. 30ECh. 10.6 - Prob. 31ECh. 10.6 - Prob. 32ECh. 10.6 - Prob. 33ECh. 10.6 - Prob. 34ECh. 10.6 - Prob. 35ECh. 10.6 - Prob. 36ECh. 10.6 - Prob. 37ECh. 10.6 - Prob. 38ECh. 10.6 - Prob. 39ECh. 10.6 - Prob. 40ECh. 10.6 - Prob. 41ECh. 10.6 - Prob. 42ECh. 10.6 - Prob. 43ECh. 10.6 - Prob. 44ECh. 10.6 - Prob. 45ECh. 10.6 - Prob. 46ECh. 10.6 - Prob. 47ECh. 10.6 - Prob. 48ECh. 10.6 - Prob. 49ECh. 10.6 - Prob. 50ECh. 10.6 - Prob. 51ECh. 10.6 - Prob. 52ECh. 10.6 - Prob. 53ECh. 10.6 - Prob. 54ECh. 10.6 - Area of a Region In Exercises 55-58, use the...Ch. 10.6 - Prob. 56ECh. 10.6 - Prob. 57ECh. 10.6 - Prob. 58ECh. 10.6 - Prob. 59ECh. 10.6 - Prob. 60ECh. 10.6 - Prob. 61ECh. 10.6 - Prob. 62ECh. 10.6 - Prob. 63ECh. 10.6 - Prob. 64ECh. 10.6 - Prob. 65ECh. 10.6 - Comet Hale-Bopp The comet Hale-Bopp has an...Ch. 10.6 - Eccentricity In Exercises 67 and 68, let r0...Ch. 10.6 - Prob. 68ECh. 10 - Matching In Exercises 1-6, match the equation with...Ch. 10 - Matching In Exercises 16, match the equation with...Ch. 10 - Prob. 3RECh. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Prob. 6RECh. 10 - Prob. 7RECh. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Prob. 11RECh. 10 - Prob. 12RECh. 10 - Prob. 13RECh. 10 - Prob. 14RECh. 10 - Prob. 15RECh. 10 - Prob. 16RECh. 10 - Prob. 17RECh. 10 - Prob. 18RECh. 10 - Prob. 19RECh. 10 - Prob. 20RECh. 10 - Prob. 21RECh. 10 - Prob. 22RECh. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - Prob. 25RECh. 10 - Prob. 26RECh. 10 - Prob. 27RECh. 10 - Prob. 28RECh. 10 - Prob. 29RECh. 10 - Prob. 30RECh. 10 - Prob. 31RECh. 10 - Prob. 32RECh. 10 - Prob. 33RECh. 10 - Prob. 34RECh. 10 - Prob. 35RECh. 10 - Prob. 36RECh. 10 - Prob. 37RECh. 10 - Prob. 38RECh. 10 - Prob. 39RECh. 10 - Prob. 40RECh. 10 - Prob. 41RECh. 10 - Prob. 42RECh. 10 - Prob. 43RECh. 10 - Prob. 44RECh. 10 - Prob. 45RECh. 10 - Prob. 46RECh. 10 - Prob. 47RECh. 10 - Prob. 48RECh. 10 - Prob. 49RECh. 10 - Prob. 50RECh. 10 - Horizontal and Vertical Tangency In Exercises...Ch. 10 - Prob. 52RECh. 10 - Prob. 53RECh. 10 - Prob. 54RECh. 10 - Prob. 55RECh. 10 - Prob. 56RECh. 10 - Prob. 57RECh. 10 - Prob. 58RECh. 10 - Prob. 59RECh. 10 - Prob. 60RECh. 10 - Prob. 61RECh. 10 - Prob. 62RECh. 10 - Prob. 63RECh. 10 - Rectangular-to-Polar Conversion In Exercises...Ch. 10 - Prob. 65RECh. 10 - Prob. 66RECh. 10 - Prob. 67RECh. 10 - Prob. 68RECh. 10 - Prob. 69RECh. 10 - Prob. 70RECh. 10 - Prob. 71RECh. 10 - Prob. 72RECh. 10 - Prob. 73RECh. 10 - Prob. 74RECh. 10 - Prob. 75RECh. 10 - Prob. 76RECh. 10 - Prob. 77RECh. 10 - Prob. 78RECh. 10 - Prob. 79RECh. 10 - Prob. 80RECh. 10 - Prob. 81RECh. 10 - Prob. 82RECh. 10 - Prob. 83RECh. 10 - Prob. 84RECh. 10 - Prob. 85RECh. 10 - Prob. 86RECh. 10 - Prob. 87RECh. 10 - Prob. 88RECh. 10 - Prob. 89RECh. 10 - Prob. 90RECh. 10 - Prob. 91RECh. 10 - Prob. 92RECh. 10 - Prob. 93RECh. 10 - Prob. 94RECh. 10 - Prob. 95RECh. 10 - Prob. 96RECh. 10 - Finding the Area of a Polar Region In Exercises...Ch. 10 - Prob. 98RECh. 10 - Prob. 99RECh. 10 - Prob. 100RECh. 10 - Prob. 101RECh. 10 - Prob. 102RECh. 10 - Prob. 103RECh. 10 - Prob. 104RECh. 10 - Prob. 105RECh. 10 - Prob. 106RECh. 10 - Prob. 107RECh. 10 - Prob. 108RECh. 10 - Prob. 109RECh. 10 - Prob. 110RECh. 10 - Prob. 111RECh. 10 - Prob. 112RECh. 10 - Prob. 113RECh. 10 - Prob. 114RECh. 10 - Prob. 115RECh. 10 - Prob. 116RECh. 10 - Prob. 117RECh. 10 - Prob. 118RECh. 10 - Prob. 119RECh. 10 - Prob. 120RECh. 10 - Prob. 121RECh. 10 - Prob. 122RECh. 10 - Prob. 123RECh. 10 - Prob. 124RECh. 10 - Prob. 125RECh. 10 - Prob. 126RECh. 10 - Prob. 1PSCh. 10 - Prob. 2PSCh. 10 - Prob. 3PSCh. 10 - Flight Paths An air traffic controller spots two...Ch. 10 - Prob. 5PSCh. 10 - Prob. 6PSCh. 10 - Cornu Spiral Consider the cornu spiral given by...Ch. 10 - Prob. 8PSCh. 10 - Prob. 9PSCh. 10 - Prob. 10PSCh. 10 - Prob. 11PSCh. 10 - Prob. 12PSCh. 10 - Prob. 13PSCh. 10 - Prob. 14PSCh. 10 - Prob. 15PSCh. 10 - Prob. 16PSCh. 10 - Prob. 17PS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 1. Find the area of the region enclosed between the curves y = x and y = x. Sketch the region.arrow_forwardfor the given rectangular coordinates, find two sets of polar coordinates for which 0≤θ<2π, one with r>0 and the other with r<0. (-2sqrt(3),9)arrow_forwardI circled the correct answer, could you show me how to do it using divergence and polar coordinatesarrow_forward
- The correct answer is D Could you explain and show the steps pleasearrow_forwardTaylor Series Approximation Example- H.W More terms used implies better approximation f(x) 4 f(x) Zero order f(x + 1) = f(x;) First order f(x; + 1) = f(x;) + f'(x;)h 1.0 Second order 0.5 True f(x + 1) = f(x) + f'(x)h + ƒ"(x;) h2 2! f(x+1) 0 x; = 0 x+1 = 1 x h f(x)=0.1x4-0.15x³- 0.5x2 -0.25x + 1.2 51 Taylor Series Approximation H.w: Smaller step size implies smaller error Errors f(x) + f(x,) Zero order f(x,+ 1) = f(x) First order 1.0 0.5 Reduced step size Second order True f(x + 1) = f(x) + f'(x)h f(x; + 1) = f(x) + f'(x)h + "(xi) h2 f(x,+1) O x₁ = 0 x+1=1 Using Taylor Series Expansion estimate f(1.35) with x0 =0.75 with 5 iterations (or & s= 5%) for f(x)=0.1x 0.15x³-0.5x²- 0.25x + 1.2 52arrow_forwardCould you explain this using the formula I attached and polar coorindatesarrow_forward
- Let g(z) = z-i z+i' (a) Evaluate g(i) and g(1). (b) Evaluate the limits lim g(z), and lim g(z). 2-12 (c) Find the image of the real axis under g. (d) Find the image of the upper half plane {z: Iz > 0} under the function g.arrow_forwardk (i) Evaluate k=7 k=0 [Hint: geometric series + De Moivre] (ii) Find an upper bound for the expression 1 +2x+2 where z lies on the circle || z|| = R with R > 10. [Hint: Use Cauchy-Schwarz]arrow_forward21. Determine for which values of m the function (x) = x™ is a solution to the given equation. a. 3x2 d²y dx² b. x2 d²y +11x dy - 3y = 0 dx dy dx2 x dx 5y = 0arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY