Calculus, Early Transcendentals
Calculus, Early Transcendentals
9th Edition
ISBN: 9781337613927
Author: Stewart
Publisher: CENGAGE L
bartleby

Concept explainers

Minimization
In mathematics, traditional optimization problems are typically expressed in terms of minimization. When we talk about minimizing or maximizing a function, we refer to the maximum and minimum possible values of that function. This can be expressed in ter…
Maxima and Minima
The extreme points of a function are the maximum and the minimum points of the function. A maximum is attained when the function takes the maximum value and a minimum is attained when the function takes the minimum value.
Derivatives
A derivative means a change. Geometrically it can be represented as a line with some steepness. Imagine climbing a mountain which is very steep and 500 meters high. Is it easier to climb? Definitely not! Suppose walking on the road for 500 meters. Which …
Concavity
In calculus, concavity is a descriptor of mathematics that tells about the shape of the graph. It is the parameter that helps to estimate the maximum and minimum value of any of the functions and the concave nature using the graphical method. We use the …
bartleby

Videos

Textbook Question
Book Icon
Chapter 10.2, Problem 5E

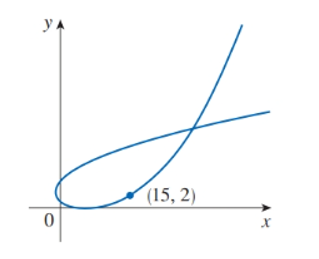
Find the slope of the tangent to the parametric curve at the indicated point.

5. x = t 2 + 2 t ,   y = 2 t − 2 t

Chapter 10.2, Problem 5E, Find the slope of the tangent to the parametric curve at the indicated point. 5. x=t2+2t,y=2t2t

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 10.2, Problem 4E
Next
Chapter 10.2, Problem 6E
Students have asked these similar questions
5. The graph of ƒ is given below. Sketch a graph of f'. 6. The graph of ƒ is given below. Sketch a graph of f'. 0 x 7. The graph of ƒ is given below. List the x-values where f is not differentiable. 0 A 2 4
2. DRAW a picture, label using variables to represent each component, set up an equation to relate the variables, then differentiate the equation to solve the problem below. The top of a ladder slides down a vertical wall at a rate of 0.15 m/s. At the moment when the bottom of the ladder is 3 m from the wall, it slides away from the wall at a rate of 0.2 m/s. How long is the ladder?
Please answer all questions and show full credit please

Chapter 10 Solutions

Calculus, Early Transcendentals

Ch. 10.1 - Prob. 1ECh. 10.1 - For the given parametric equations, find the...Ch. 10.1 - Sketch the curve by using the parametric equations...Ch. 10.1 - Sketch the curve by using the parametric equations...Ch. 10.1 - Prob. 7ECh. 10.1 - Prob. 8ECh. 10.1 - Prob. 9ECh. 10.1 - Prob. 10ECh. 10.1 - Prob. 11ECh. 10.1 - Prob. 12E
Ch. 10.1 - Prob. 16ECh. 10.1 - Prob. 17ECh. 10.1 - Prob. 22ECh. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - Describe the motion of a particle with position...Ch. 10.1 - Describe the motion of a particle with position...Ch. 10.1 - Describe the motion of a particle with position...Ch. 10.1 - Describe the motion of a particle with position...Ch. 10.1 - Suppose a curve is given by the parametric...Ch. 10.1 - Match the graphs of the parametric equations x =...Ch. 10.1 - Prob. 31ECh. 10.1 - Prob. 32ECh. 10.1 - Prob. 33ECh. 10.1 - Graph the curve x = y 2 sin y.Ch. 10.1 - Graph the curves y = x3 4x and x = y3 4y and...Ch. 10.1 - (a) Show that the parametric equations x = x1 +...Ch. 10.1 - Use a graphing device and the result of Exercise...Ch. 10.1 - Find parametric equations for the position of a...Ch. 10.1 - Prob. 40ECh. 10.1 - Find parametric equations for the path of a...Ch. 10.1 - (a) Find parametric equations for the ellipse...Ch. 10.1 - Use a graphing calculator or computer to reproduce...Ch. 10.1 - Use a graphing calculator or computer to reproduce...Ch. 10.1 - Derive Equations 1 for the case /2Ch. 10.1 - Let P be a point at a distance d from the center...Ch. 10.1 - If a and b are fixed numbers, find parametric...Ch. 10.1 - If a and b are fixed numbers, find parametric...Ch. 10.1 - A curve, called a witch of Maria Agnesi, consists...Ch. 10.1 - (a) Find parametric equations for the set of all...Ch. 10.1 - Investigate the family of curves defined by the...Ch. 10.1 - The swallowtail catastrophe curves are defined by...Ch. 10.1 - Graph several members of the family of curves with...Ch. 10.1 - Graph several members of the family of curves x =...Ch. 10.1 - Prob. 63ECh. 10.1 - Prob. 64ECh. 10.2 - Find dx/dt,dy/dt, and dy/dx. 1. x=2t3+3t,y=4t5t2Ch. 10.2 - Find dx/dt,dy/dt, and dy/dx. 2. x=tlnt,y=t2t2Ch. 10.2 - Prob. 3ECh. 10.2 - Prob. 4ECh. 10.2 - Find the slope of the tangent to the parametric...Ch. 10.2 - Find the slope of the tangent to the parametric...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find the points on the curve where the tangent is...Ch. 10.2 - Find the points on the curve where the tangent is...Ch. 10.2 - Find the points on the curve where the tangent is...Ch. 10.2 - Find the points on the curve where the tangent is...Ch. 10.2 - Use a graph to estimate the coordinates of the...Ch. 10.2 - Prob. 26ECh. 10.2 - Graph the curve in a viewing rectangle that...Ch. 10.2 - Graph the curve in a viewing rectangle that...Ch. 10.2 - Show that the curve x = cos t, y = sin t cos t has...Ch. 10.2 - Prob. 30ECh. 10.2 - At what point(s) on the curve x = 3t2 + 1, y = t3 ...Ch. 10.2 - Find equations of the tangents to the curve x =...Ch. 10.2 - Use the parametric equations of an ellipse, x = a...Ch. 10.2 - Let be the region enclosed by the loop of the...Ch. 10.2 - Find the exact length of the curve. 42. x = et t,...Ch. 10.2 - Find the exact length of the curve. 43. x = t sin...Ch. 10.2 - Find the exact length of the curve. 44. x = 3 cos...Ch. 10.2 - Graph the curve and find its exact length. 45. x =...Ch. 10.2 - Graph the curve and find its exact length. 46....Ch. 10.2 - Graph the curve x = sin t + sin 1.5t, y = cos t...Ch. 10.2 - Find the length of the loop of the curve x = 3t ...Ch. 10.2 - Prob. 57ECh. 10.2 - Prob. 58ECh. 10.2 - Prob. 59ECh. 10.2 - Prob. 60ECh. 10.2 - The curve shown in the figure is the astroid...Ch. 10.2 - Set up an integral that represents the area of the...Ch. 10.2 - Prob. 68ECh. 10.2 - Prob. 69ECh. 10.2 - Prob. 70ECh. 10.2 - Find the exact area of the surface obtained by...Ch. 10.2 - Find the exact area of the surface obtained by...Ch. 10.2 - Find the exact area of the surface obtained by...Ch. 10.2 - Prob. 74ECh. 10.2 - Find the surface area generated by rotating the...Ch. 10.2 - Prob. 76ECh. 10.2 - Prob. 77ECh. 10.2 - Prob. 78ECh. 10.2 - A cow is tied to a silo with radius r by a rope...Ch. 10.3 - Plot the point whose polar coordinates are given....Ch. 10.3 - Prob. 2ECh. 10.3 - Plot the point whose polar coordinates are given....Ch. 10.3 - Plot the point whose polar coordinates are given....Ch. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Prob. 7ECh. 10.3 - Prob. 8ECh. 10.3 - Sketch the region in the plane consisting of...Ch. 10.3 - Prob. 10ECh. 10.3 - Sketch the region in the plane consisting of...Ch. 10.3 - Prob. 12ECh. 10.3 - Find the distance between the points with polar...Ch. 10.3 - Prob. 14ECh. 10.3 - Identify the curve by finding a Cartesian equation...Ch. 10.3 - Prob. 16ECh. 10.3 - Identify the curve by finding a Cartesian equation...Ch. 10.3 - Identify the curve by finding a Cartesian equation...Ch. 10.3 - Identify the curve by finding a Cartesian equation...Ch. 10.3 - Prob. 20ECh. 10.3 - Prob. 21ECh. 10.3 - Prob. 22ECh. 10.3 - Prob. 23ECh. 10.3 - Prob. 24ECh. 10.3 - Prob. 25ECh. 10.3 - Find a polar equation for the curve represented by...Ch. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Prob. 29ECh. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Prob. 36ECh. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Prob. 38ECh. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Prob. 48ECh. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Prob. 50ECh. 10.3 - Prob. 51ECh. 10.3 - Show that the curve r = 2 csc (also a conchoid)...Ch. 10.3 - Show that the curve r = sin tan (called a...Ch. 10.3 - Sketch the curve (x2 + y2)3 = 4x2y2.Ch. 10.3 - Prob. 57ECh. 10.3 - Show that the curves r = a sin and r = a cos ...Ch. 10.3 - Prob. 59ECh. 10.3 - Prob. 60ECh. 10.3 - Prob. 61ECh. 10.3 - Prob. 62ECh. 10.3 - Prob. 63ECh. 10.3 - Graph the polar curve. Choose a parameter interval...Ch. 10.3 - Prob. 65ECh. 10.3 - Prob. 66ECh. 10.3 - Prob. 67ECh. 10.3 - Prob. 68ECh. 10.4 - Find the area of the region that is bounded by the...Ch. 10.4 - Find the area of the region that is bounded by the...Ch. 10.4 - Find the area of the region that is bounded by the...Ch. 10.4 - Find the area of the region that is bounded by the...Ch. 10.4 - Find the area of the shaded region. 5.Ch. 10.4 - Find the area of the shaded region. 6.Ch. 10.4 - Find the area of the shaded region. 7.Ch. 10.4 - Find the area of the shaded region. 8.Ch. 10.4 - Sketch the curve and find the area that it...Ch. 10.4 - Sketch the curve and find the area that it...Ch. 10.4 - Prob. 11ECh. 10.4 - Prob. 12ECh. 10.4 - Graph the curve and find the area that it...Ch. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Find the area of the region enclosed by one loop...Ch. 10.4 - Find the area of the region enclosed by one loop...Ch. 10.4 - Find the area of the region enclosed by one loop...Ch. 10.4 - Find the area of the region enclosed by one loop...Ch. 10.4 - Find the area of the region enclosed by one loop...Ch. 10.4 - Find the area enclosed by the loop of the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Prob. 34ECh. 10.4 - Find the area inside the larger loop and outside...Ch. 10.4 - Find the area between a large loop and the...Ch. 10.4 - Find all points of intersection of the given...Ch. 10.4 - Find all points of intersection of the given...Ch. 10.4 - Find all points of intersection of the given...Ch. 10.4 - Prob. 40ECh. 10.4 - Find all points of intersection of the given...Ch. 10.4 - Prob. 42ECh. 10.4 - Prob. 43ECh. 10.4 - The points of intersection of the cardioid r = 1 +...Ch. 10.4 - When recording live performances, sound engineers...Ch. 10.4 - Find the exact length of the polar curve. 45. r =...Ch. 10.4 - Find the exact length of the polar curve. 47. r =...Ch. 10.4 - Find the exact length of the polar curve. 48. r =...Ch. 10.4 - Find the exact length of the curve. Use a graph to...Ch. 10.4 - Find the exact length of the curve. Use a graph to...Ch. 10.4 - Use a calculator to find the length of the curve...Ch. 10.4 - Prob. 60ECh. 10.4 - Prob. 61ECh. 10.4 - Prob. 62ECh. 10.4 - Prob. 65ECh. 10.4 - Prob. 67ECh. 10.4 - Find the points on the given curve where the...Ch. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Prob. 3ECh. 10.5 - Prob. 6ECh. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Find an equation of the parabola. Then find the...Ch. 10.5 - Find an equation of the parabola. Then find the...Ch. 10.5 - Prob. 11ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Prob. 20ECh. 10.5 - Prob. 21ECh. 10.5 - Prob. 22ECh. 10.5 - Prob. 23ECh. 10.5 - Prob. 24ECh. 10.5 - Prob. 25ECh. 10.5 - Prob. 26ECh. 10.5 - Identify the type of conic section whose equation...Ch. 10.5 - Identify the type of conic section whose equation...Ch. 10.5 - Prob. 29ECh. 10.5 - Prob. 30ECh. 10.5 - Prob. 31ECh. 10.5 - Identify the type of conic section whose equation...Ch. 10.5 - Prob. 33ECh. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - Prob. 37ECh. 10.5 - Prob. 38ECh. 10.5 - Prob. 39ECh. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Prob. 41ECh. 10.5 - Prob. 42ECh. 10.5 - Prob. 43ECh. 10.5 - Prob. 44ECh. 10.5 - Prob. 45ECh. 10.5 - Prob. 46ECh. 10.5 - Prob. 47ECh. 10.5 - Prob. 48ECh. 10.5 - Prob. 49ECh. 10.5 - Prob. 50ECh. 10.5 - The point in a lunar orbit nearest the surface of...Ch. 10.5 - A cross-section of a parabolic reflector is shown...Ch. 10.5 - The LORAN (LOng RAnge Navigation) radio navigation...Ch. 10.5 - Use the definition of a hyperbola to derive...Ch. 10.5 - Show that the function defined by the upper branch...Ch. 10.5 - Find an equation for the ellipse with foci (1, 1)...Ch. 10.5 - Determine the type of curve represented by the...Ch. 10.5 - Prob. 58ECh. 10.5 - Prob. 59ECh. 10.5 - Prob. 60ECh. 10.5 - Prob. 61ECh. 10.5 - Prob. 62ECh. 10.5 - Find the area of the region enclosed by the...Ch. 10.5 - Prob. 64ECh. 10.5 - Find the centroid of the region enclosed by the...Ch. 10.5 - Prob. 66ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Prob. 7ECh. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - Prob. 11ECh. 10.6 - Prob. 12ECh. 10.6 - Prob. 13ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - Prob. 16ECh. 10.6 - Prob. 17ECh. 10.6 - Prob. 18ECh. 10.6 - Prob. 19ECh. 10.6 - Prob. 20ECh. 10.6 - Prob. 21ECh. 10.6 - Prob. 22ECh. 10.6 - Prob. 23ECh. 10.6 - Prob. 24ECh. 10.6 - Prob. 25ECh. 10.6 - Prob. 26ECh. 10.6 - Prob. 27ECh. 10.6 - Prob. 28ECh. 10.6 - Prob. 29ECh. 10.6 - Prob. 30ECh. 10.6 - Prob. 31ECh. 10.6 - Jupiter's orbit has eccentricity 0.048 and the...Ch. 10.6 - The orbit of Halleys comet, last seen in 1986 and...Ch. 10.6 - Prob. 34ECh. 10.6 - Prob. 35ECh. 10.6 - Prob. 36ECh. 10.6 - Prob. 37ECh. 10 - (a) What is a parametric curve? (b) How do you...Ch. 10 - Prob. 2CCCh. 10 - Prob. 3CCCh. 10 - Prob. 5CCCh. 10 - Prob. 6CCCh. 10 - Prob. 7CCCh. 10 - Prob. 8CCCh. 10 - Prob. 9CCCh. 10 - (a) What is the eccentricity of a conic section?...Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Prob. 6TFQCh. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Prob. 1ECh. 10 - Prob. 2ECh. 10 - Prob. 3ECh. 10 - Prob. 4ECh. 10 - Prob. 5ECh. 10 - Prob. 7ECh. 10 - Prob. 8ECh. 10 - Prob. 9ECh. 10 - Prob. 10ECh. 10 - Prob. 11ECh. 10 - Prob. 12ECh. 10 - Prob. 13ECh. 10 - Sketch the polar curve. 12. r = 3 + cos 3Ch. 10 - Prob. 15ECh. 10 - Prob. 16ECh. 10 - Prob. 17ECh. 10 - Prob. 18ECh. 10 - Prob. 19ECh. 10 - Prob. 20ECh. 10 - The curve with polar equation r = (sin )/ is...Ch. 10 - Prob. 23ECh. 10 - Prob. 24ECh. 10 - Prob. 25ECh. 10 - Prob. 26ECh. 10 - Prob. 27ECh. 10 - Prob. 28ECh. 10 - Prob. 29ECh. 10 - Prob. 30ECh. 10 - Prob. 31ECh. 10 - Prob. 32ECh. 10 - Find the area enclosed by the curve r2 = 9 cos 5.Ch. 10 - Prob. 34ECh. 10 - Prob. 35ECh. 10 - Prob. 36ECh. 10 - Find the area of the region that lies inside both...Ch. 10 - Find the area of the region that lies inside the...Ch. 10 - Prob. 39ECh. 10 - Prob. 40ECh. 10 - Prob. 41ECh. 10 - Prob. 42ECh. 10 - Prob. 45ECh. 10 - Prob. 46ECh. 10 - Prob. 47ECh. 10 - Prob. 48ECh. 10 - Prob. 49ECh. 10 - Prob. 50ECh. 10 - Prob. 51ECh. 10 - Prob. 52ECh. 10 - Prob. 53ECh. 10 - Prob. 54ECh. 10 - Prob. 55ECh. 10 - Prob. 56ECh. 10 - Prob. 57ECh. 10 - Prob. 58ECh. 10 - Prob. 59ECh. 10 - Prob. 61ECh. 10 - A curve called the folium of Descartes is defined...Ch. 10 - The outer circle in the figure has radius 1 and...Ch. 10 - Prob. 2PPCh. 10 - Prob. 3PPCh. 10 - Four bugs are placed at the four corners of a...Ch. 10 - Prob. 5PPCh. 10 - A circle C of radius 2r has its center at the...
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Text book image
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Finding Local Maxima and Minima by Differentiation; Author: Professor Dave Explains;https://www.youtube.com/watch?v=pvLj1s7SOtk;License: Standard YouTube License, CC-BY