
Concept explainers
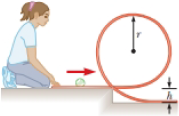
A tennis ball is a hollow sphere with a thin wall. It is set rolling without slipping at 4.03 m/s on a horizontal section of a track as shown in Figure P10.33. It rolls around the inside of a vertical circular loop of radius r = 45.0 cm. As the ball nears the bottom of the loop, the shape of the track deviates from a perfect circle so that the ball leaves the track at a point h = 20.0 cm below the horizontal section. (a) Find the ball’s speed at the top of the loop. (b) Demonstrate that the ball will not fall from the track at the top of the loop. (c) Find the ball’s speed as it leaves the track at the bottom. (d) What If? Suppose that static friction between ball and track were negligible so that the ball slid instead of rolling. Describe the speed of the ball at the top of the loop in this situation. (e) Explain your answer to part (d).
Figure P10.33
(a)
The speed of the ball at the top of the loop.
Answer to Problem 33P
The speed of the ball at the top of the loop is
Explanation of Solution
The radius of the circular loop is
Write the expression for the law of energy conservation between horizontal track and the top of the loop
Here,
Write the expression for the translational kinetic energy of the ball at horizontal track
Here,
Write the expression for the rotational kinetic energy of the ball at horizontal track
Here,
Write the expression for the moment of inertia of the ball
Write the expression for the initial angular speed of the ball
Substitute
Write the expression for the translational kinetic energy of the ball at top point of the loop
Here,
Write the expression for the rotational kinetic energy of the ball at top point of the loop
Here,
Write the expression for the moment of inertia of the ball
Write the expression for the initial angular speed of the ball
Substitute
Write the expression for the potential energy of the ball at top point of the loop
Here,
Substitute
Simplify the above equation for
Conclusion:
Substitute
Therefore, the speed of the ball at the top of the loop is
(b)
The reason that the ball will not fall from the track at the top of the loop.
Answer to Problem 33P
The ball will not fall because the value of the centripetal acceleration is more than the acceleration due to gravity at the top point of the circular loop.
Explanation of Solution
The radius of the circular loop is
Formula to calculate the centripetal acceleration on the ball at the top of the loop
Here,
Substitute
Thus, the centripetal acceleration act on the ball at the top of the loop is
Since the centripetal acceleration at the top of the loop is more than the acceleration due to gravity that is
Conclusion:
Therefore, the ball will not fall because the value of the centripetal acceleration is more than the acceleration due to gravity at the top point of the circular loop.
(c)
The speed of the ball as it leaves the track at the bottom.
Answer to Problem 33P
The speed of the ball as it leaves the track at the bottom is
Explanation of Solution
The radius of the circular loop is
Write the expression for the law of energy conservation between horizontal track and the bottom of the loop
Here,
Write the expression for the translational kinetic energy of the ball at bottom point of the loop
Here,
Write the expression for the rotational kinetic energy of the ball at bottom point of the loop
Here,
Write the expression for the initial angular speed of the ball
Substitute
Write the expression for the potential energy of the ball at top point of the loop
Here,
Substitute
Simplify the above equation for
Conclusion:
Substitute
Thus, the speed of the ball as it leaves the track at the bottom is
(d)
The speed of the ball at the top of the loop if ball slide instead of roll.
Answer to Problem 33P
The speed of the ball at the top of the loop is imaginary.
Explanation of Solution
Write the expression for the law of energy conservation between horizontal track and the top of the loop
Here,
Write the expression for the rotational kinetic energy of the ball at horizontal track
Write the expression for the new translational kinetic energy of the ball at top point of the loop
Here,
Write the expression for the new potential energy of the ball at top point of the loop
Substitute
Simplify the above equation for
Substitute
Since the value inside the square root is negative that means the value is imaginary. This condition is impractical.
Thus, the speed of the ball at the top of the loop is imaginary.
Conclusion:
Therefore, the speed of the ball at the top of the loop is imaginary. It can’t be calculated.
(e)
The explanation of the solution of part (d).
Answer to Problem 33P
The ball has not sufficient energy to arrive at top of the circular loop.
Explanation of Solution
The velocity comes out to be imaginary in part (d) that indicates the situation in impossible because as the boll slide instead of rolling, the ball have only translational kinetic energy which is insufficient for the ball to reach the top point on the circular loop.
Thus, the ball did not arrive at the top point of the loop.
Conclusion:
Therefore, the ball has not sufficient energy to arrive at top of the circular loop.
Want to see more full solutions like this?
Chapter 10 Solutions
PHYSICS FOR SCI.AND ENGR W/WEBASSIGN
- Mick and Rick are twins born on Earth in the year 2175. Rick grows up to be an Earth-bound robotics technician while Mick becomes an intergalactic astronaut. Mick leaves the Earth on his first space mission in the year 2200 and travels, according to his clock, for 10 years at a speed of 0.75c. Unfortunately, at this point in his journey, the structure of his ship undergoes mechanical breakdown and the ship explodes. How old is Rick when his brother dies?arrow_forwardHi, I have canceled, why did you charge me again?arrow_forwardNo chatgpt pls will upvotearrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





