
(a)
To find: The variables IBI and area using numerical method.
(a)
Answer to Problem 32E
Solution: The obtained result can be shown in tabular form as follows:
Variable |
Mean |
Standard deviation |
Area |
28.29 |
17.71 |
IBI |
65.94 |
18.28 |
Explanation of Solution
Calculation: Calculate the average and standard deviation of IBI and area using Minitab as follows:
Step 1: Enter the data in Minitab.
Step 2: Click on Stat --> Basic statistics --> Display
Step 3: Double click on “Area” and “IBI” to move it to variables column.
Step 4: Click on “Statistics” and check the box for mean and standard deviation.
Step 5: Click “OK” twice to obtain the result.
Results are obtained as
Variable |
Mean |
Standard deviation |
Area |
28.29 |
17.71 |
IBI |
65.94 |
18.28 |
To find: The variables IBI and area using graphical method.
Answer to Problem 32E
Solution: The graph of “Area” is slightly right skewed and the graph of “IBI” is left skewed.
Explanation of Solution
Graph: Construct the histograms to check the skewness using Minitab as follows:
Step 1: Go to Graphs > Histogram > Simple histogram.
Step 2: Double click on “Area” and “IBI” to move it to variables column.
Step 3: Click “OK” to obtain the result.
The graph is obtained as
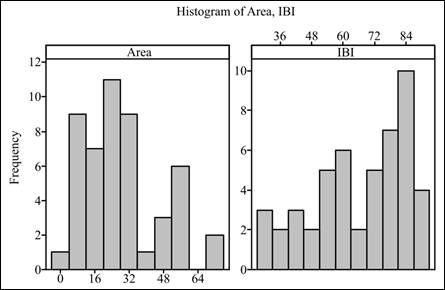
Interpretation: The graph of area is slightly right skewed and the graph of IBI is left skewed.
(b)
To graph: A
(b)
Explanation of Solution
Graph: Construct a scatter plot as follows:
Step 1: Enter the data in Minitab.
Step 2: Click on Graph --> Scatterplot. Select scatterplot with regression.
Step 3: Double click on “IBI” to move it Y variable and “Area” to move it to X variable column.
Step 4: Click “OK” twice to obtain the graph.
The scatter plot is obtained as
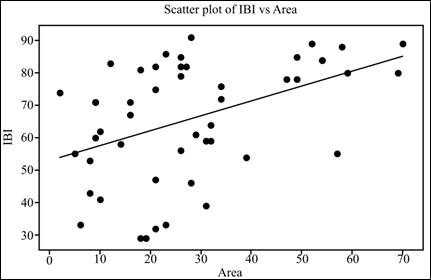
Interpretation: The graph shows weak linear relationship between IBI and Area with no unusual activity.
(c)
To explain: The statistical model for simple linear regression.
(c)
Answer to Problem 32E
Solution: The model is
Explanation of Solution
where
(d)
To explain: The null and alternate hypotheses.
(d)
Answer to Problem 32E
Solution: The null and alternative hypotheses are
Explanation of Solution
So, the null and alternative hypotheses can be stated as
(e)
To test: The least square
(e)
Answer to Problem 32E
Solution: The obtained output represents that the P-value is less than 0.05. So there is enough evidence for the linearity in the regression line.
Explanation of Solution
Calculation: Obtain the regression line using Minitab as follows:
Step 1: Enter the data in Minitab.
Step 2: Click on Stat --> Regression --> Regression.
Step 3: Double click on “IBI” to move it response column and “Area” to move it to predictor column.
Step 4: Click “OK” to obtain the result.
The results are obtained.
Conclusion: From the obtained output, the value of test statistic is 3.42 and the P-value is 0.001. Since the P-value is less than the significance level 0.05, it can be concluded that there is enough evidence for the linearity in the regression line.
(f)
To find: The residuals.
(f)
Answer to Problem 32E
Solution: The residuals are as follows:
Area |
IBI |
Residuals |
21 |
47 |
–15.5862 |
34 |
76 |
7.4318 |
6 |
33 |
–22.6839 |
47 |
78 |
3.4497 |
10 |
62 |
4.4755 |
49 |
78 |
2.5294 |
23 |
33 |
–30.5065 |
32 |
64 |
–3.6479 |
12 |
83 |
24.5552 |
16 |
67 |
6.7146 |
29 |
61 |
–5.2675 |
49 |
85 |
9.5294 |
28 |
46 |
–19.8073 |
8 |
53 |
–3.6042 |
57 |
55 |
–24.1518 |
9 |
71 |
13.9356 |
31 |
59 |
–8.1878 |
10 |
41 |
–16.5245 |
21 |
82 |
19.4138 |
26 |
56 |
–8.8870 |
31 |
39 |
–28.1878 |
52 |
89 |
12.1490 |
21 |
32 |
–30.5862 |
8 |
43 |
–13.6042 |
18 |
29 |
–32.2058 |
5 |
55 |
–0.2237 |
18 |
81 |
19.7942 |
26 |
82 |
17.1130 |
27 |
82 |
16.6529 |
26 |
85 |
20.1130 |
32 |
59 |
–8.6479 |
2 |
74 |
20.1567 |
59 |
80 |
–0.0721 |
58 |
88 |
8.3880 |
19 |
29 |
–32.6659 |
14 |
58 |
–1.3651 |
16 |
71 |
10.7146 |
9 |
60 |
2.9356 |
23 |
86 |
22.4935 |
28 |
91 |
25.1927 |
34 |
72 |
3.4318 |
70 |
89 |
3.8662 |
69 |
80 |
–4.6737 |
54 |
84 |
6.2287 |
39 |
54 |
–16.8690 |
9 |
71 |
13.9356 |
21 |
75 |
12.4138 |
54 |
84 |
6.2287 |
26 |
79 |
14.1130 |
Explanation of Solution
Calculation: Obtain the regression line using Minitab as follows:
Step 1: Enter the data in Minitab.
Step 2: Click on Stat --> Regression --> Regression.
Step 3: Double click on “IBI” to move it to response column and “Area” to move it to predictor column.
Step 4: Click on “Storage” and check the box for residuals.
Step 5: Click “OK” twice to obtain the result.
To graph: The scatterplot.
Explanation of Solution
Graph: Construct a scatterplot using Minitab as follows:
Step 1: Enter the data in Minitab.
Step 2: Click on Graph --> Scatterplot. Select scatterplot with regression.
Step 3: Double click on “Area” to move it X variable and “Residuals” to move it to Y variable column.
Step 4: Click “OK” to obtain the graph.
The scatter plot is obtained as
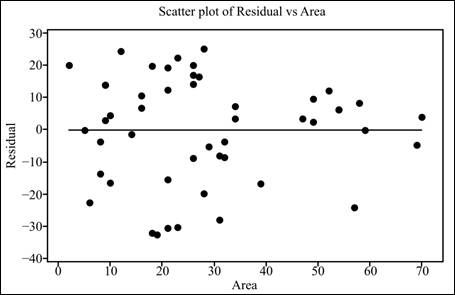
Interpretation: The graph shows that there is more variation for small
Whether there is something unusual.
Answer to Problem 32E
Solution: No, there is nothing unusual.
Explanation of Solution
(g)
That residuals are normal or not.
(g)
Answer to Problem 32E
Solution: The residuals are
Explanation of Solution
Step 1: Click on Stat --> Descriptive statistics --> Normality test.
Step 2: Double click on “Residuals” to move it to the variable column.
Step 3: Click “OK” to obtain the graph.
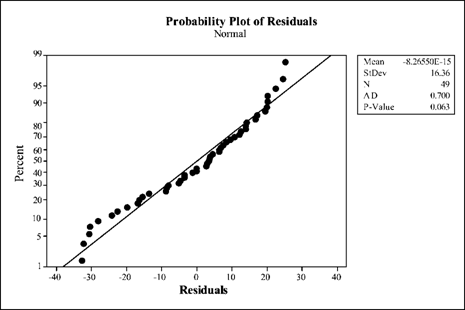
Conclusion: All the points lie near the trend line and there are no outliers. Therefore, it can be concluded that residuals are normally distributed.
(h)
If the assumptions of statistical inference are satisfied or not.
(h)
Answer to Problem 32E
Solution: The assumptions are satisfied.
Explanation of Solution
Want to see more full solutions like this?
Chapter 10 Solutions
EBK INTRODUCTION TO THE PRACTICE OF STA
- Question: A company launches two different marketing campaigns to promote the same product in two different regions. After one month, the company collects the sales data (in units sold) from both regions to compare the effectiveness of the campaigns. The company wants to determine whether there is a significant difference in the mean sales between the two regions. Perform a two sample T-test You can provide your answer by inserting a text box and the answer must include: Null hypothesis, Alternative hypothesis, Show answer (output table/summary table), and Conclusion based on the P value. (2 points = 0.5 x 4 Answers) Each of these is worth 0.5 points. However, showing the calculation is must. If calculation is missing, the whole answer won't get any credit.arrow_forwardBinomial Prob. Question: A new teaching method claims to improve student engagement. A survey reveals that 60% of students find this method engaging. If 15 students are randomly selected, what is the probability that: a) Exactly 9 students find the method engaging?b) At least 7 students find the method engaging? (2 points = 1 x 2 answers) Provide answers in the yellow cellsarrow_forwardIn a survey of 2273 adults, 739 say they believe in UFOS. Construct a 95% confidence interval for the population proportion of adults who believe in UFOs. A 95% confidence interval for the population proportion is ( ☐, ☐ ). (Round to three decimal places as needed.)arrow_forward
- Find the minimum sample size n needed to estimate μ for the given values of c, σ, and E. C=0.98, σ 6.7, and E = 2 Assume that a preliminary sample has at least 30 members. n = (Round up to the nearest whole number.)arrow_forwardIn a survey of 2193 adults in a recent year, 1233 say they have made a New Year's resolution. Construct 90% and 95% confidence intervals for the population proportion. Interpret the results and compare the widths of the confidence intervals. The 90% confidence interval for the population proportion p is (Round to three decimal places as needed.) J.D) .arrow_forwardLet p be the population proportion for the following condition. Find the point estimates for p and q. In a survey of 1143 adults from country A, 317 said that they were not confident that the food they eat in country A is safe. The point estimate for p, p, is (Round to three decimal places as needed.) ...arrow_forward
- (c) Because logistic regression predicts probabilities of outcomes, observations used to build a logistic regression model need not be independent. A. false: all observations must be independent B. true C. false: only observations with the same outcome need to be independent I ANSWERED: A. false: all observations must be independent. (This was marked wrong but I have no idea why. Isn't this a basic assumption of logistic regression)arrow_forwardBusiness discussarrow_forwardSpam filters are built on principles similar to those used in logistic regression. We fit a probability that each message is spam or not spam. We have several variables for each email. Here are a few: to_multiple=1 if there are multiple recipients, winner=1 if the word 'winner' appears in the subject line, format=1 if the email is poorly formatted, re_subj=1 if "re" appears in the subject line. A logistic model was fit to a dataset with the following output: Estimate SE Z Pr(>|Z|) (Intercept) -0.8161 0.086 -9.4895 0 to_multiple -2.5651 0.3052 -8.4047 0 winner 1.5801 0.3156 5.0067 0 format -0.1528 0.1136 -1.3451 0.1786 re_subj -2.8401 0.363 -7.824 0 (a) Write down the model using the coefficients from the model fit.log_odds(spam) = -0.8161 + -2.5651 + to_multiple + 1.5801 winner + -0.1528 format + -2.8401 re_subj(b) Suppose we have an observation where to_multiple=0, winner=1, format=0, and re_subj=0. What is the predicted probability that this message is spam?…arrow_forward
- Consider an event X comprised of three outcomes whose probabilities are 9/18, 1/18,and 6/18. Compute the probability of the complement of the event. Question content area bottom Part 1 A.1/2 B.2/18 C.16/18 D.16/3arrow_forwardJohn and Mike were offered mints. What is the probability that at least John or Mike would respond favorably? (Hint: Use the classical definition.) Question content area bottom Part 1 A.1/2 B.3/4 C.1/8 D.3/8arrow_forwardThe details of the clock sales at a supermarket for the past 6 weeks are shown in the table below. The time series appears to be relatively stable, without trend, seasonal, or cyclical effects. The simple moving average value of k is set at 2. What is the simple moving average root mean square error? Round to two decimal places. Week Units sold 1 88 2 44 3 54 4 65 5 72 6 85 Question content area bottom Part 1 A. 207.13 B. 20.12 C. 14.39 D. 0.21arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





