
Concept explainers
Analyze and find all the reactions of the frame.
Explanation of Solution
Determine the deflection position of AB and BA using the relation;
Determine the deflection position of BC and CB using the relation;
Determine the end moment of each member as shown below;
Apply Equilibrium at joint B;
Apply Equilibrium at joint C;
Solve Equation (1) and (2).
Calculation of end moment of each member as shown below;
Hence, the end moment of member AB is
Hence, the end moment of member BA is
Hence, the end moment of member BC is
Hence, the end moment of member CB is
Hence, the end moment of member BE is
Hence, the end moment of member EB is
Hence, the end moment of member CD is
Hence, the end moment of member DC is
Show the free body diagram of support A, span AB, span BC, span EB, and span DC as in Figure (1).
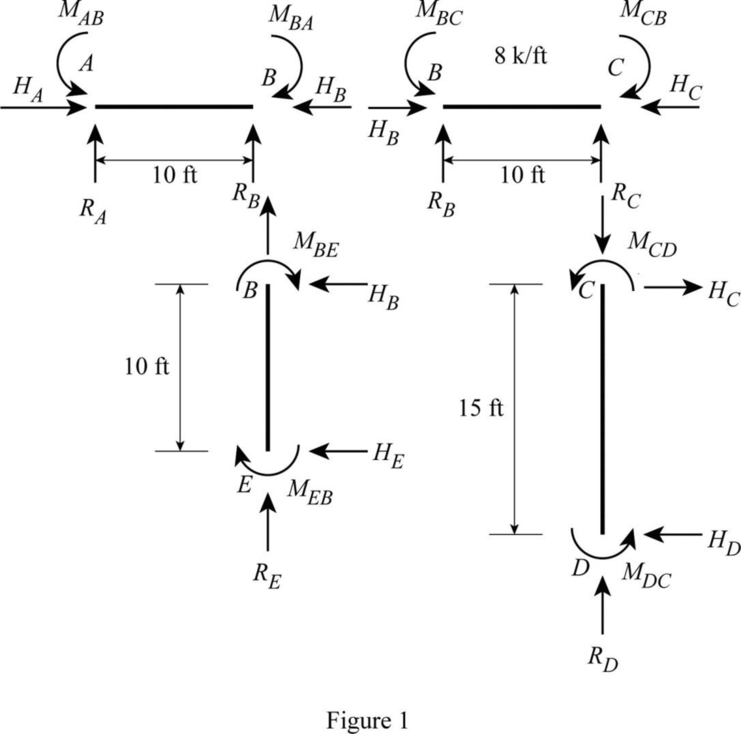
Consider span AB;
Consider clockwise moment is positive and counterclockwise moment is negative.
Determine the vertical reaction at support B;
Take moment about point A;
Consider upward is positive and downward is negative.
Determine the vertical reaction at A;
Hence, the vertical reaction at A is
Consider span BC;
Determine the vertical reaction at support C;
Take moment about point B;
Determine the vertical reaction at B;
Hence, the total reaction at B is
Consider span BE;
Refer Figure (1),
The vertical reaction of 30.8 kips acts as upward reaction at B.
Determine the vertical reaction at E;
Determine the horizontal reaction E;
Take moment about B;
Determine the horizontal reaction at B;
Consider span CD;
Refer Figure (1),
The vertical reaction 12.2 kips at point C will acts downward reaction at C.
Determine the vertical reaction at E;
Hence, the vertical reaction at D is
Determine the horizontal reaction D;
Take moment about C;
Determine the horizontal reaction at C;
Determine the horizontal force at A and B for span AB;
Want to see more full solutions like this?
Chapter 10 Solutions
Fundamentals Of Structural Analysis:
- 1. For the system shown below, calculate the power supplied to the pump if its efficiency is 82%. Methyl alcohol at 25°C is flowing at the rate of 50m³/hour. The suction line is a standard DN100 schedule 40 steel pipe, 15m long. The total length of DN50 schedule 40 steel pipe in the discharge line is 180m. Assume that the entrance from reservoir 1 is through a square-edged inlet and that the elbows are standard. The valve is a fully open globe valve. 12m Discharge line DN 50 schedule 40 steel Pump Suction line Fully open globe valve DN 100 schedule 40 steel Flow Standard elbows (2)arrow_forwardDetermine rotations at all the nodes of the beam and reactions at the supports using stiffness method. Assume support 1 and 3 are roller and support 2 is pinned, L1=1.25m, L2=3.75m and w=60kN/m. Please show all working and FBD's where relevant.arrow_forwardDraw the BMD of the beam on the compression side showing the salient values. What are the maximum bending moments of the beam? Draw the deflected shape of the beam. Assume support 1 and 3 are roller and support 2 is pinned, L1=1.25m, L2=3.75m and w=60kN/m.arrow_forward
- Size a flash and floc tank: Provide a sketch with dimensions and calculations Provide for vertical mixers Size the mixer and motor Flow Rate 33 MGD Peaking Factor 1.5 Use VDH Regs (Online) Low Temp 40 degrees High Temp = 70 degrees Redundant Tanksarrow_forwardI do not know how to solve this questionarrow_forwardI don't know how to solve this questionarrow_forward
- A national pricing service says the National price is $12.35 per unit. The adjusted price adjustment for Los Angeles is 1.15. The price adjustment for Tulsa is 0.94. What is the expected price difference between Tulsa and Los Angeles? c.$2.98 b.$2.59 d.$0.00 a.$0.21arrow_forwardPROBLEM: Design the transversely reinforced concrete deck slab shown in the cross-sectional detail below. 8" REINFORCED CONCRETE SLAB 1/4" PER FT. T 3-3% 8'-0" 8'-0" 4'-0" GIVEN: Bridge to carry two traffic lanes. Concrete strength =4.5 ksi. Grade 60 reinforcement f, = 60 ksi. Account for 25 psf future wearing surface. Assume stringers are W36 x 150. Deck has a 0.5 in integrated wearing surface.arrow_forwardPlease help me answer this questionarrow_forward
- I need help solving this problem, I'm not sure how to draw these diagrams.arrow_forwardI need help solving this problemarrow_forward88 L Solle ined sove in peaper 96252 Example 5.5 The turbine rotor of a ship has a mass of 30 tons, a radius of gyration of 600 mm and rotates at 2400 rpm in a clockwise direction when viewed from aft. The ship pitches through a total angle of 15%, 7.5° above and 7.5° below the horizontal, the motion being simple harmonic and having a period of 12 sec. Determine the maximum gyroscopic couple on the holding down bolts of the turbine and the direction of yaw as the bow rises. النص ملصقات -20125 750 31 الرسم X 7.0! 989 Carrow_forward

 Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON
Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
 Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning
Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning





