Chapter 10, Problem 1RE

In Problems 1-4, find all critical points and determine whether they are relative maxima, relative minima, or horizontal points of inflection.

$y=-x^2$

To determine

To calculate: The critical values, relative maxima, relative minima, or horizontal points of inflection of the function $y=-x^2$ by using the derivative.

Answer to Problem 1RE

Solution:

The critical value(s) are $x=0$, the relative maxima is $x=\left(0,0\right)$, the relative minima is not there and the horizontal point of inflection is not there.

Explanation of Solution

Given Information:

The provided equation is $y=-x^2$.

Formula Used:

The critical values are the only values at which the graph can have turning points, the derivative cannot change sign anywhere except at the critical value.

This, in an interval between two critical values, the sign of the derivative at any value in the interval will be the sign of the derivative at all values in the interval.

As per the First Derivative Test,

The first derivative of the function is evaluated. The first derivative is made equal to zero in order to get the critical points.

The values of the critical values are kept inside the original function which gives the critical points. The intervals of the values of x are then evaluated for the relative maximum and minimum.

Calculation:

Consider the provided equation $y=-x^2$,

The critical values are the only values at which the graph can have turning points, the derivative cannot change sign anywhere except at the critical value.

Hence, there will no change in the values of critical values as in the derivative graph.

Take out the first derivative of the equation by the power rule,

$y^{\prime }=-2x$

Put the value of $y^{\prime }=0$,

$\begin{array}{c}{y}^{\prime }=-2x=0\\ =x=0\end{array}$

Hence, the values of x are $x=0$.

Evaluate the values of the original functions with the critical values:

Put $x=0$ in the equation $y=-x^2$,

$\begin{array}{c}y=-{\left(0\right)}^2\\ =0\end{array}$

Hence, $x=\left(0,0\right)$ is a critical point.

The relative maximum can be evaluated as follows by two ways, it can be understood as reaching a peak after increasing, and then going for a downfall.

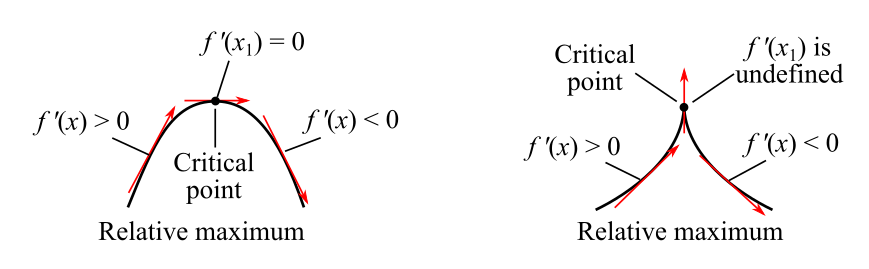
It can be observed that there is $x=\left(0,0\right)$ as relative maxima.

The relative minimum can be evaluated as follows by two ways, it can be understood as reaching a peak after decreasing, and then going upward.

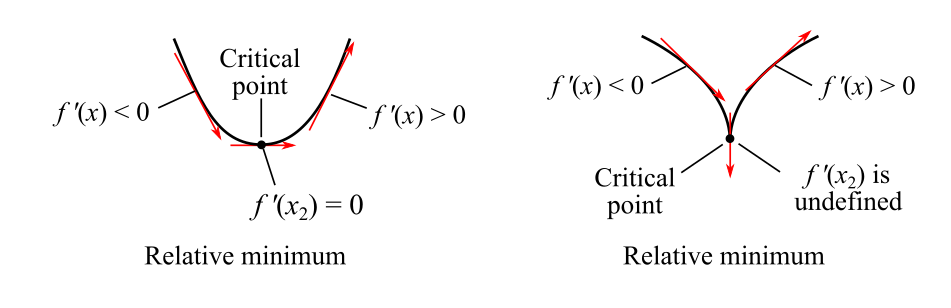
It can be observed that there is no relative minima.

If the first derivative of f is 0 at $x_0$ but does not change from positive to negative or from negative to positive as x passes through $x_0$, then the critical point at $x_0$ is neither a relative maximum nor a relative minimum.

In this case, it is said that f has a horizontal point of inflection.

The horizontal point of inflection is not there.