Chapter 10, Problem 10.26E

For a particle in a state having the wavefunction

$\Psi =\sqrt{\frac{2}{a}}\sin \frac{\pi \text{x}}{a}$ in the range $x=0\text{to}a$, what is the probability that the particle exists in the following intervals?

(a) $x=0\text{to}0.02a$ (b) $x=0.24a\text{to}0.26a$

(c) $x=0.49a\text{to}0.51a$ (d) $x=0.74a\text{to}0.76a$

(e) $x=0.98a\text{to}1.00a$

Plot the probabilities versus $x$. What does your plot illustrate about the probability?

Interpretation Introduction

(a)

Interpretation:

The probability for the particle having wavefunction $\Psi =\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}$ in the range of $x=0\text{to}0.02a$ is to be calculated.

Concept introduction:

For the normalization of the wavefunction, the wavefunction is integrated as a product of its conjugate over the entire limits. It is expressed by the equation as given below.

${\displaystyle \underset{0}{\overset{\infty }{\int }}\left(N\Psi \right)\left(N{\Psi }^{*}\right)}=1$

Where,

• $N$ is the normalization constant

• ${\Psi }^{*}$ is the conjugate of the wavefunction

• $\Psi$ is the wavefunction

Answer to Problem 10.26E

The probability for the particle having wavefunction $\Psi =\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}$ in the range of $x=0\text{to}0.02a$ is $5.57\times {10}^{-5}$.

Explanation of Solution

For the probability of the wavefunction the expression is as follows.

${\displaystyle \underset{0}{\overset{\infty }{\int }}\left(N\Psi \right)\left(N{\Psi }^{*}\right)}=P$

Where,

• $N$ is the normalization constant

• ${\Psi }^{*}$ is the conjugate of the wavefunction

• $\Psi$ is the wavefunction

• $P$ is the probability

Substitute the values in the above equation as follows.

$\begin{array}{rll}P& =& {\displaystyle \underset{0}{\overset{0.02a}{\int }}\left(\Psi \right)\left({\Psi }^{*}\right)}dx\\ & =& {\displaystyle \underset{0}{\overset{0.02a}{\int }}\left(\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}\right)\left(\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}\right)}dx\\ & =& \frac{2}{a}{\displaystyle \underset{0}{\overset{0.02a}{\int }}\left(\sin \frac{\pi x}{a}\right)\left(\sin \frac{\pi x}{a}\right)}dx\\ & =& \frac{2}{a}{\displaystyle \underset{0}{\overset{0.02a}{\int }}{\left(\sin \frac{\pi x}{a}\right)}^{2}dx}\end{array}$

The above expression is simplified as follows.

$\begin{array}{rll}& =& \frac{2}{a}{\displaystyle \underset{0}{\overset{0.02a}{\int }}\left({\sin }^2\frac{\pi x}{a}\right)dx}\\ & =& \frac{2}{a}\times {\left[\frac{x}{2}-\frac{a}{4\pi }\sin \frac{2\pi x}{a}\right]}_0^{0.02a}\\ & =& \frac{2}{a}\times \left[\left(\frac{0.02a}{2}-\frac{a}{4\pi }\sin \frac{2\pi \left(0.02a\right)}{a}\right)-0\right]\\ & =& \frac{2}{a}\times \left(\frac{0.02a}{2}-\frac{a}{4\pi }\sin 0.04\pi \right)\end{array}$

$\begin{array}{l}=\frac{2}{a}\times \left(\frac{0.02a}{2}-\frac{a}{12.56}\sin \left(0.1256\right)\right)\\ =\frac{2}{a}\times \left(\frac{0.02a}{2}-\frac{0.12527a}{12.56}\right)\\ =\frac{2}{a}\times \frac{0.0007a}{25.12}\\ =5.57\times {10}^{-5}\end{array}$

Conclusion

The probability for the particle having wavefunction $\Psi =\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}$ in the range of $x=0to0.02a$ is calculated as $5.57\times {10}^{-5}$.

Interpretation Introduction

(b)

Interpretation:

The probability for the particle having wavefunction $\Psi =\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}$ in the range of $x=0.24a\text{to}0.26a$ is to be calculated.

Concept introduction:

For the normalization of the wavefunction, the wavefunction is integrated as a product of its conjugate over the entire limits. It is expressed by the equation as given below.

${\displaystyle \underset{0}{\overset{\infty }{\int }}\left(N\Psi \right)\left(N{\Psi }^{*}\right)}=1$

Where,

• $N$ is the normalization constant

• ${\Psi }^{*}$ is the conjugate of the wavefunction

• $\Psi$ is the wavefunction

Answer to Problem 10.26E

The probability for the particle having wavefunction $\Psi =\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}$ in the range of $\text{x}=0.24a\text{to}0.26a$ is $0.0199$.

Explanation of Solution

For the probability of the wavefunction the expression is as follows.

${\displaystyle \underset{0}{\overset{\infty }{\int }}\left(N\Psi \right)\left(N{\Psi }^{*}\right)}=P$

Where,

• $N$ is the normalization constant

• ${\Psi }^{*}$ is the conjugate of the wavefunction

• $\Psi$ is the wavefunction

• $P$ is the probability

Substitute the values in the above equation as follows.

$\begin{array}{rll}P& =& {\displaystyle \underset{0.24a}{\overset{0.26a}{\int }}\left(\Psi \right)\left({\Psi }^{*}\right)}dx\\ & =& {\displaystyle \underset{0.24a}{\overset{0.26a}{\int }}\left(\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}\right)\left(\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}\right)}dx\\ & =& \frac{2}{a}{\displaystyle \underset{0.24a}{\overset{0.26a}{\int }}\left(\sin \frac{\pi x}{a}\right)\left(\sin \frac{\pi x}{a}\right)}dx\\ & =& \frac{2}{a}{\displaystyle \underset{0.24a}{\overset{0.26a}{\int }}{\left(\sin \frac{\pi x}{a}\right)}^{2}dx}\end{array}$

The above expression is simplified as follows.

$\begin{array}{rll}& =& \frac{2}{a}{\displaystyle \underset{0.24a}{\overset{0.26a}{\int }}\left({\sin }^2\frac{\pi x}{a}\right)dx}\\ & =& \frac{2}{a}\times {\left[\frac{x}{2}-\frac{a}{4\pi }\sin \frac{2\pi x}{a}\right]}_{0.24a}^{0.26a}\\ & =& \frac{2}{a}\times \left[\left(\frac{0.26a}{2}-\frac{a}{4\pi }\sin \frac{2\pi \left(0.26a\right)}{a}\right)-\left(\frac{0.24a}{2}-\frac{a}{4\pi }\sin \frac{2\pi \left(0.24a\right)}{a}\right)\right]\\ & =& \frac{2}{a}\times \left(\frac{0.26a}{2}-\frac{0.24a}{2}-\frac{a}{4\pi }\sin 0.52\pi +\frac{a}{4\pi }\sin 0.48\pi \right)\end{array}$

$\begin{array}{l}==\frac{2}{a}\times \left(\frac{0.26a}{2}-\frac{0.24a}{2}-\frac{a}{4\pi }\sin 0.52\pi +\frac{a}{4\pi }\sin 0.48\pi \right)\\ =\frac{2}{a}\times \left(\frac{0.02a}{2}-\frac{0.0001a}{12.56}\right)\\ =\frac{2}{a}\times \frac{0.251a}{25.12}\\ =0.0199\end{array}$

Conclusion

The probability for the particle having wavefunction $\Psi =\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}$ in the range of $x=0.24a\text{to}0.26a$ is calculated as $0.0199$.

Interpretation Introduction

(c)

Interpretation:

The probability for the particle having wavefunction $\Psi =\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}$ in the range of $\text{x}=0.49a\text{to}0.51a$ is to be calculated.

Concept introduction:

For the normalization of the wavefunction, the wavefunction is integrated as a product of its conjugate over the entire limits. It is expressed by the equation as given below.

${\displaystyle \underset{0}{\overset{\infty }{\int }}\left(N\Psi \right)\left(N{\Psi }^{*}\right)}=1$

Where,

• $N$ is the normalization constant

• ${\Psi }^{*}$ is the conjugate of the wavefunction

• $\Psi$ is the wavefunction

Answer to Problem 10.26E

The probability for the particle having wavefunction $\Psi =\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}$ in the range of $\text{x}=0.49a\text{to}0.51a$ is $0.0399$.

Explanation of Solution

For the probability of the wavefunction the expression is as follows.

${\displaystyle \underset{0}{\overset{\infty }{\int }}\left(N\Psi \right)\left(N{\Psi }^{*}\right)}=P$

Where,

• $N$ is the normalization constant

• ${\Psi }^{*}$ is the conjugate of the wavefunction

• $\Psi$ is the wavefunction

• $P$ is the probability

Substitute the values in the above equation as follows.

$\begin{array}{rll}P& =& {\displaystyle \underset{0.49a}{\overset{0.51a}{\int }}\left(\Psi \right)\left({\Psi }^{*}\right)}dx\\ & =& {\displaystyle \underset{0.49a}{\overset{0.51a}{\int }}\left(\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}\right)\left(\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}\right)}dx\\ & =& \frac{2}{a}{\displaystyle \underset{0.49a}{\overset{0.51a}{\int }}\left(\sin \frac{\pi x}{a}\right)\left(\sin \frac{\pi x}{a}\right)}dx\\ & =& \frac{2}{a}{\displaystyle \underset{0.49a}{\overset{0.51a}{\int }}{\left(\sin \frac{\pi x}{a}\right)}^{2}dx}\end{array}$

The above expression is simplified as follows.

$\begin{array}{rll}& =& \frac{2}{a}{\displaystyle \underset{0.49a}{\overset{0.51a}{\int }}\left({\sin }^2\frac{\pi x}{a}\right)dx}\\ & =& \frac{2}{a}\times {\left[\frac{x}{2}-\frac{a}{4\pi }\sin \frac{2\pi x}{a}\right]}_{0.49a}^{0.51a}\\ & =& \frac{2}{a}\times \left[\left(\frac{0.51a}{2}-\frac{a}{4\pi }\sin \frac{2\pi \left(0.51a\right)}{a}\right)-\left(\frac{0.49a}{2}-\frac{a}{4\pi }\sin \frac{2\pi \left(0.49a\right)}{a}\right)\right]\\ & =& \frac{2}{a}\times \left(\frac{0.51a}{2}-\frac{0.49a}{2}-\frac{a}{4\pi }\sin 1.02\pi +\frac{a}{4\pi }\sin 0.98\pi \right)\end{array}$

$\begin{array}{l}=\frac{2}{a}\times \left(\left(\frac{0.51a}{2}-\frac{0.49a}{2}\right)-\frac{a}{4\pi }\sin 1.02\pi +\frac{a}{4\pi }\sin 0.98\pi \right)\\ =\frac{2}{a}\times \left(\frac{0.02a}{2}+\frac{0.125517a}{12.56}\right)\\ =\frac{2}{a}\times \frac{0.502234a}{25.12}\\ =0.0399\end{array}$

Conclusion

The probability for the particle having wavefunction $\Psi =\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}$ in the range of $\text{x}=0.49a\text{to}0.51a$ is calculated as $0.0399$.

Interpretation Introduction

(d)

Interpretation:

The probability for the particle having wavefunction $\Psi =\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}$ in the range of $\text{x}=0.74a\text{to}0.76a$ is to be calculated.

Concept introduction:

For the normalization of the wavefunction, the wavefunction is integrated as a product of its conjugate over the entire limits. It is expressed by the equation as given below.

${\displaystyle \underset{0}{\overset{\infty }{\int }}\left(N\Psi \right)\left(N{\Psi }^{*}\right)}=1$

Where,

• $N$ is the normalization constant

• ${\Psi }^{*}$ is the conjugate of the wavefunction

• $\Psi$ is the wavefunction

Answer to Problem 10.26E

The probability for the particle having wavefunction $\Psi =\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}$ in the range of $\text{x}=0.74a\text{to}0.76a$ is $0.0204$.

Explanation of Solution

For the probability of the wavefunction the expression is as follows.

${\displaystyle \underset{0}{\overset{\infty }{\int }}\left(N\Psi \right)\left(N{\Psi }^{*}\right)}=P$

Where,

• $N$ is the normalization constant

• ${\Psi }^{*}$ is the conjugate of the wavefunction

• $\Psi$ is the wavefunction

• $P$ is the probability

Substitute the values in the above equation as follows.

$\begin{array}{rll}P& =& {\displaystyle \underset{0.74a}{\overset{0.76a}{\int }}\left(\Psi \right)\left({\Psi }^{*}\right)}dx\\ & =& {\displaystyle \underset{0.74a}{\overset{0.76a}{\int }}\left(\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}\right)\left(\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}\right)}dx\\ & =& \frac{2}{a}{\displaystyle \underset{0.74a}{\overset{0.76a}{\int }}\left(\sin \frac{\pi x}{a}\right)\left(\sin \frac{\pi x}{a}\right)}dx\\ & =& \frac{2}{a}{\displaystyle \underset{0.74a}{\overset{0.76a}{\int }}{\left(\sin \frac{\pi x}{a}\right)}^{2}dx}\end{array}$

The above expression is simplified as follows.

$\begin{array}{rll}& =& \frac{2}{a}{\displaystyle \underset{0.74a}{\overset{0.76a}{\int }}\left({\sin }^2\frac{\pi x}{a}\right)dx}\\ & =& \frac{2}{a}\times {\left[\frac{x}{2}-\frac{a}{4\pi }\sin \frac{2\pi x}{a}\right]}_{0.74a}^{0.76a}\\ & =& \frac{2}{a}\times \left[\left(\frac{0.76a}{2}-\frac{a}{4\pi }\sin \frac{2\pi \left(0.76a\right)}{a}\right)-\left(\frac{0.74a}{2}-\frac{a}{4\pi }\sin \frac{2\pi \left(0.74a\right)}{a}\right)\right]\\ & =& \frac{2}{a}\times \left(\frac{0.76a}{2}-\frac{0.74a}{2}-\frac{a}{4\pi }\sin 1.52\pi +\frac{a}{4\pi }\sin 1.48\pi \right)\end{array}$

$\begin{array}{l}=\frac{2}{a}\times \left(\left(\frac{0.76a}{2}-\frac{0.74a}{2}\right)-\frac{a}{4\pi }\sin 1.52\pi +\frac{a}{4\pi }\sin 1.48\pi \right)\\ =\frac{2}{a}\times \left(\frac{0.02a}{2}+\frac{0.003a}{12.56}\right)\\ =\frac{2}{a}\times \frac{0.2572a}{25.12}\\ =0.0204\end{array}$

Conclusion

The probability for the particle having wavefunction $\Psi =\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}$ in the range of $\text{x}=0.74a\text{to}0.76a$ is calculated as $0.0204$.

Interpretation Introduction

(e)

Interpretation:

The probability for the particle having wavefunction $\Psi =\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}$ in the range of $\text{x}=0.98a\text{to}1.00a$ is to be calculated. The graph of probabilities versus $x$ is to be plotted.

Concept introduction:

For the normalization of the wavefunction, the wavefunction is integrated as a product of its conjugate over the entire limits. It is expressed by the equation as given below.

${\displaystyle \underset{0}{\overset{\infty }{\int }}\left(N\Psi \right)\left(N{\Psi }^{*}\right)}=1$

Where,

• $N$ is the normalization constant

• ${\Psi }^{*}$ is the conjugate of the wavefunction

• $\Psi$ is the wavefunction

Answer to Problem 10.26E

The probability for the particle having wavefunction $\Psi =\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}$ in the range of $\text{x}=0.98a\text{to}1.00a$ is $5\times {10}^{-5}$.The graph of probabilities versus $x$ is given below.

Explanation of Solution

For the probability of the wavefunction the expression is as follows.

${\displaystyle \underset{0}{\overset{\infty }{\int }}\left(N\Psi \right)\left(N{\Psi }^{*}\right)}=P$

Where,

• $N$ is the normalization constant

• ${\Psi }^{*}$ is the conjugate of the wavefunction

• $\Psi$ is the wavefunction

• $P$ is the probability

Substitute the values in the above equation as follows.

$\begin{array}{rll}P& =& {\displaystyle \underset{0.98a}{\overset{1a}{\int }}\left(\Psi \right)\left({\Psi }^{*}\right)}dx\\ & =& {\displaystyle \underset{0.98a}{\overset{1a}{\int }}\left(\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}\right)\left(\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}\right)}dx\\ & =& \frac{2}{a}{\displaystyle \underset{0.98a}{\overset{1a}{\int }}\left(\sin \frac{\pi x}{a}\right)\left(\sin \frac{\pi x}{a}\right)}dx\\ & =& \frac{2}{a}{\displaystyle \underset{0.98a}{\overset{1a}{\int }}{\left(\sin \frac{\pi x}{a}\right)}^{2}dx}\end{array}$

The above expression is simplified as follows.

$\begin{array}{rll}& =& \frac{2}{a}{\displaystyle \underset{0.98a}{\overset{1a}{\int }}\left({\sin }^2\frac{\pi x}{a}\right)dx}\\ & =& \frac{2}{a}\times {\left[\frac{x}{2}-\frac{a}{4\pi }\sin \frac{2\pi x}{a}\right]}_{0.98a}^{1a}\\ & =& \frac{2}{a}\times \left[\left(\frac{a}{2}-\frac{a}{4\pi }\sin \frac{2\pi \left(a\right)}{a}\right)-\left(\frac{0.98a}{2}-\frac{a}{4\pi }\sin \frac{2\pi \left(0.98a\right)}{a}\right)\right]\\ & =& \frac{2}{a}\times \left(\frac{a}{2}-\frac{0.98a}{2}-\frac{a}{4\pi }\sin 2\pi +\frac{a}{4\pi }\sin 1.96\pi \right)\end{array}$

$\begin{array}{l}=\frac{2}{a}\times \left(\left(\frac{a}{2}-\frac{0.98a}{2}\right)-\frac{a}{4\pi }\sin 2\pi +\frac{a}{4\pi }\sin 1.96\pi \right)\\ =\frac{2}{a}\times \left(\frac{0.02a}{2}-\frac{0.125244a}{12.56}\right)\\ =\frac{2}{a}\times \left(\frac{0.000712a}{25.12}\right)\\ =5\times {10}^{-5}\end{array}$

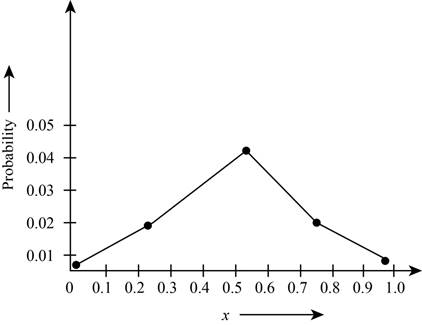
Theplot the probabilities versus $x$ is given in figure 1.

Figure 1

The plot shows the probability for the given wave function. According to this plot, the probability of finding the particle is maximum in the range of $x=0.49a\text{to}0.51a$. Also, the plot gives the curve for the sine function as given.

Conclusion

The probability for the particle having wavefunction $\Psi =\sqrt{\frac{2}{a}}\sin \frac{\pi x}{a}$ in the range of $\text{x}=0.98a\text{to}1.00a$ is calculated as $5\times {10}^{-5}$.