zN-1 = (z-5°)(z-GN-1). Exercise 5. 1. By computing the coefficient of zN-1 on the right hand side of the above equation, show that the sum of Nth roots of unity is equal to 0. 2. (This one is harder) Compute the coefficient of zN-2 on the right-hand side of the above equation. What property of the N'th roots of unity can you conclude from this?
zN-1 = (z-5°)(z-GN-1). Exercise 5. 1. By computing the coefficient of zN-1 on the right hand side of the above equation, show that the sum of Nth roots of unity is equal to 0. 2. (This one is harder) Compute the coefficient of zN-2 on the right-hand side of the above equation. What property of the N'th roots of unity can you conclude from this?
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Please do Exercise 5 part A and B and please show step by step and explain

Transcribed Image Text:Analyzing digital signals using complex roots of unity
For the remainder of this investigation, we will take our sampling period equal to 1, and consider signals
that are linear combinations of complex waves with angular frequencies 27kf/N, where k = 0,2,... N - 1.
Notice that these are all of the waves which have positive angular frequencies less than 27 which also repeat
after N samples. Any signal s(t) that is a linear combination of these waves can be written as follows:
²nikft/N
s(t) =
N-1
k=0
The signal's information is contained in the complex amplitudes {a},k=0,...N- 1. Hence we want to
recover the amplitudes from the sampled signal.
It turns out that properties of roots of unity will be crucial in obtaining a method to recover the ampli-
tudes. To get at these properties, we will have to bring modular arithmetic also into the mix!
Let 3 = 2i/N and recall that are the Nth roots of unity for k = 0,... N-1. Since these are roots of
unity, that means they are all solutions to the equation zN - 1 = 0. This means that the linear factors z - k
all divide z - 1. Since we have N distinct linear factors, it follows that:
zN-1 = (z-5°) (z - GN-1).
Exercise 5.
1. By computing the coefficient of zN-1 on the right hand side of the above equation, show that the sum
of Nth roots of unity is equal to 0.
2. (This one is harder) Compute the coefficient of zN-2 on the right-hand side of the above equation. What
property of the N'th roots of unity can you conclude from this?
Expert Solution
Step 1
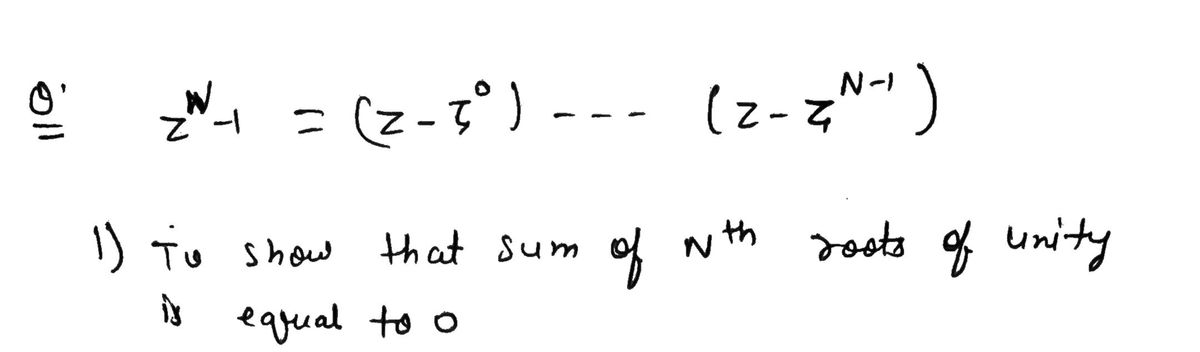
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

