Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
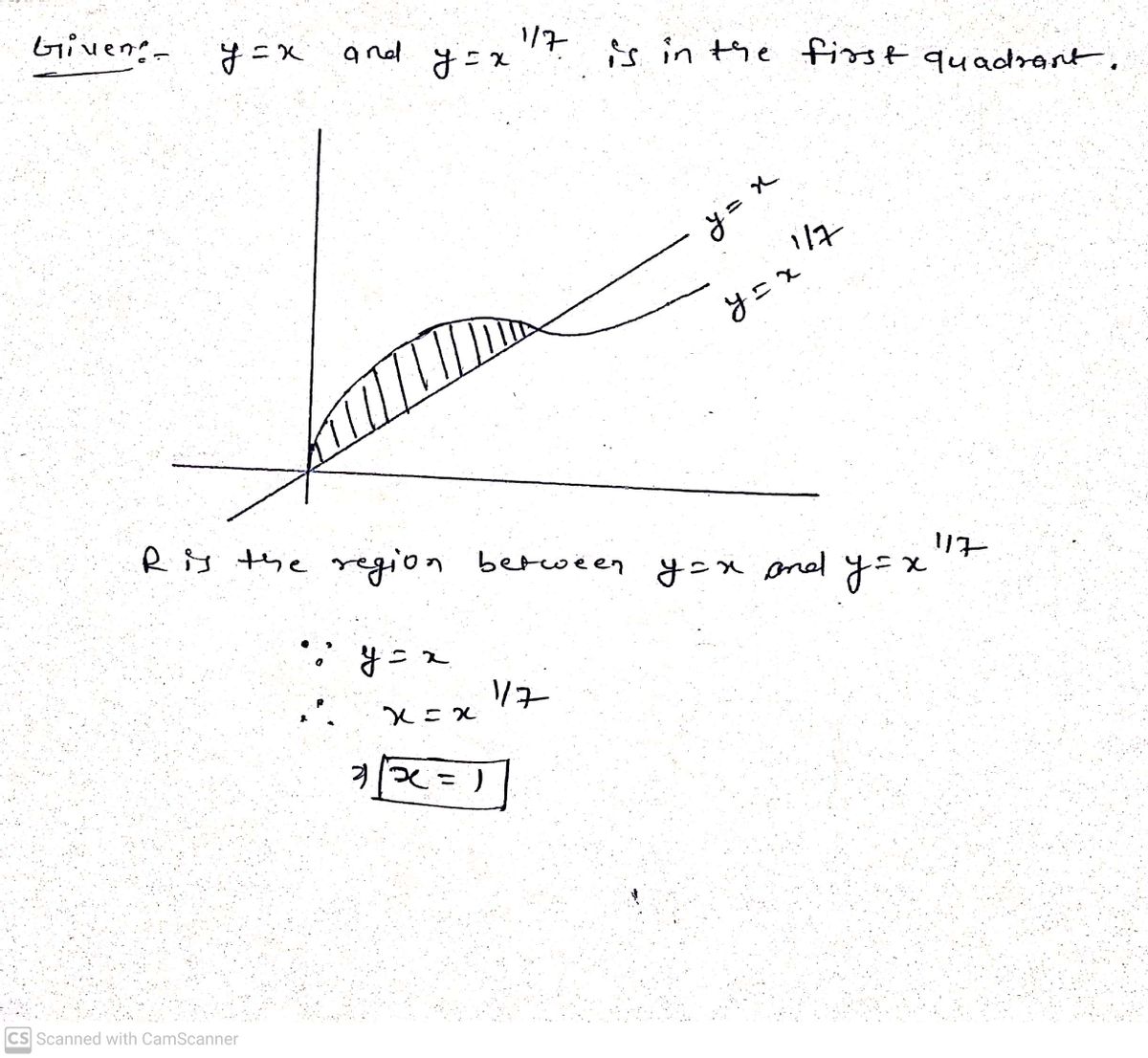
![To find the volume of the solid formed by revolving the region enclosed by the curves \( y = x \) and \( y = x^{\frac{1}{3}} \) in the first quadrant about the x-axis, we can use both the disk/washer method and the shell method. Here’s a step-by-step guide for each:
**Disk/Washer Method:**
1. **Identify the region** - The region is bounded by the curves \( y = x \) and \( y = x^{\frac{1}{3}} \) from the point where they intersect at the origin (0,0) up to their next point of intersection.
2. **Set up integral:**
- The radius of the outer circle is given by \( R = x \).
- The radius of the inner circle is given by \( r = x^{\frac{1}{3}} \).
- The volume \( V \) can be calculated using the integral:
\[
V = \pi \int (R^2 - r^2) \, dx
\]
3. **Determine limits of integration:** Find where \( y = x \) and \( y = x^{\frac{1}{3}} \) intersect again (other than the origin) and use these x-values as the limits of integration.
4. **Calculate the integral** to find the volume.
**Shell Method:**
1. **Identify the same region** as above.
2. **Set up integral:**
- The height of a representative shell is \( h = x - x^{\frac{1}{3}} \).
- The radius of a shell is \( x \).
- The volume \( V \) is given by:
\[
V = 2\pi \int x \cdot h \, dx
\]
3. **Determine limits of integration** as previously.
4. **Calculate the integral** to determine the volume.
These methods provide alternative approaches to finding the volume of a solid of revolution, each offering intuitive insights based on the geometry of the region and the axis of revolution.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F89e73a58-75a0-4c09-8c16-f2ecd1065cc1%2F1ce3bc49-1144-4586-9d37-87a69f7ce80d%2Fzvwey6t_processed.jpeg&w=3840&q=75)
Transcribed Image Text:To find the volume of the solid formed by revolving the region enclosed by the curves \( y = x \) and \( y = x^{\frac{1}{3}} \) in the first quadrant about the x-axis, we can use both the disk/washer method and the shell method. Here’s a step-by-step guide for each:
**Disk/Washer Method:**
1. **Identify the region** - The region is bounded by the curves \( y = x \) and \( y = x^{\frac{1}{3}} \) from the point where they intersect at the origin (0,0) up to their next point of intersection.
2. **Set up integral:**
- The radius of the outer circle is given by \( R = x \).
- The radius of the inner circle is given by \( r = x^{\frac{1}{3}} \).
- The volume \( V \) can be calculated using the integral:
\[
V = \pi \int (R^2 - r^2) \, dx
\]
3. **Determine limits of integration:** Find where \( y = x \) and \( y = x^{\frac{1}{3}} \) intersect again (other than the origin) and use these x-values as the limits of integration.
4. **Calculate the integral** to find the volume.
**Shell Method:**
1. **Identify the same region** as above.
2. **Set up integral:**
- The height of a representative shell is \( h = x - x^{\frac{1}{3}} \).
- The radius of a shell is \( x \).
- The volume \( V \) is given by:
\[
V = 2\pi \int x \cdot h \, dx
\]
3. **Determine limits of integration** as previously.
4. **Calculate the integral** to determine the volume.
These methods provide alternative approaches to finding the volume of a solid of revolution, each offering intuitive insights based on the geometry of the region and the axis of revolution.
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning