What is the p-value for this sample? (Report answer accurate to four decimal places.) You wish to test the following claim (Ha) at a significance level of a0.005.Н.: и — 81.5На : д + 81.5You believe the population is normally distributed, but you do not know the standard deviation. You obtain asample of size n =107 with mean M79.2 and a standard deviation of SD = 12.1.What is the test statistic for this sample? (Report answer accurate to three decimal places.)

Answered: You wish to test the following claim…

Glencoe Algebra 1, Student Edition, 9780079039897, 0079039898, 2018

18th Edition

ISBN:9780079039897

Author:Carter

Publisher:Carter

Chapter10: Statistics

Section10.5: Comparing Sets Of Data

Problem 13PPS

See similar textbooks

Related questions

Concept explainers

Question

What is the p-value for this sample? (Report answer accurate to four decimal places.)

You wish to test the following claim (Ha) at a significance level of a
0.005.
Н.: и — 81.5
На : д + 81.5
You believe the population is normally distributed, but you do not know the standard deviation. You obtain a
sample of size n =
107 with mean M
79.2 and a standard deviation of SD = 12.1.
What is the test statistic for this sample? (Report answer accurate to three decimal places.)

Expert Solution

Step 1

As the population standard deviation is not known, we will use t-test.

The provided sample mean is M = $X ˉ = 79.2$ and the sample standard deviation is S.D = $s = 12.1$ , and the sample size is $n = 107$ .

The following null and alternative hypotheses need to be tested:

Ho: μ = 81.5
Ha:μ ≠ 81.5
This corresponds to a two-tailed test.
The t-statistic is computed as follows:

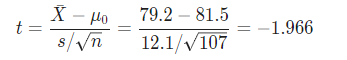
The p-value with 106 degrees of freedom and for t=-1.966 for the two-tailed test is 0.0519(from t-distribution table).
As the p-value is greater than the significance level, i.e.,0.0519≥0.005, the null hypothesis is not rejected.
Therefore, there is not enough evidence to claim that the population meanμ is different than 81.5, at the 0.005 significance level.

Step by step

Solved in 2 steps with 1 images

Knowledge Booster

$Basics of Inferential Statistics$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.

Recommended textbooks for you

Glencoe Algebra 1, Student Edition, 9780079039897…

Algebra

ISBN:

9780079039897

Author:

Carter

Publisher:

McGraw Hill