You want to obtain a sample to estimate a population proportion. Based on previous evidence, you believe the population proportion is approximately ˆp=58%p^=58%. You would like to be 99% confident that your esimate is within 0.5% of the true population proportion. How large of a sample size is required?
I have a question
You want to obtain a sample to estimate a population proportion. Based on previous evidence, you believe the population proportion is approximately ˆp=58%p^=58%. You would like to be 99% confident that your esimate is within 0.5% of the true population proportion. How large of a
Introduction:
The 100 (1 – α) % confidence interval for the population proportion, p is:
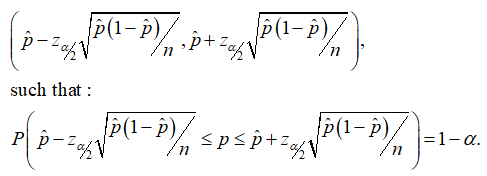
Here, n is the sample size, p̂ is the sample proportion, and zα/2 is the critical value of the standard normal distribution, above which, 100 (α/2) % or α/2 proportion of the observations lie, and below which, 100 (1 – α + α/2) % = 100 (1 – α/2) % or (1 – α/2) proportion of the observations lie.
The margin of error in this confidence interval is:
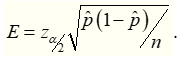
When hypothesized proportion, p is known, p̂ will be substituted by the hypothesized proportion, p in the expression for E.
Step by step
Solved in 2 steps with 4 images




