You want to obtain a sample to estimate a population mean. Based on previous evidence, you believe the population standard deviation is approximately o = 40.8. You would like to be 95% confident that your estimate is within 2.5 of the true poputation mean. How large of a sample size is required?
Inverse Normal Distribution
The method used for finding the corresponding z-critical value in a normal distribution using the known probability is said to be an inverse normal distribution. The inverse normal distribution is a continuous probability distribution with a family of two parameters.
Mean, Median, Mode
It is a descriptive summary of a data set. It can be defined by using some of the measures. The central tendencies do not provide information regarding individual data from the dataset. However, they give a summary of the data set. The central tendency or measure of central tendency is a central or typical value for a probability distribution.
Z-Scores
A z-score is a unit of measurement used in statistics to describe the position of a raw score in terms of its distance from the mean, measured with reference to standard deviation from the mean. Z-scores are useful in statistics because they allow comparison between two scores that belong to different normal distributions.
![### Estimating Sample Size for a Population Mean
To obtain a sample to estimate a population mean, consider the following scenario:
Based on prior evidence, you believe the population standard deviation to be approximately \( \sigma = 40.8 \). You aim for 95% confidence that your estimate is within 2.5 of the true population mean. The question is: **How large of a sample size is required?**
**Hint: [Video] [+]**
You will need to calculate the sample size (\( n \)) required to achieve this level of confidence.
**Input Box:**
- `n =` [ ]
**Submit Button:**
- `Submit Question`
This exercise involves understanding how sample size impacts the confidence in estimating a population parameter, particularly using known standard deviation and desired precision.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fcb64ed77-0e71-4b8d-9699-28308f43c665%2F4b6f5286-f34b-4df8-82cc-341c9c65510c%2Fjo8nd8_processed.jpeg&w=3840&q=75)
The sample size can be calculated as:
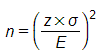
Here,
z = desired confidence level
E = The allowable margin of error ( sampling error)
σ = Population standard deviation
Given:
E = 2.5
σ = 40.8
Step by step
Solved in 2 steps with 2 images









