You are given two components, component A and component B, and suppose their lifetimes, in hours, are expo- nential with parameters XA and AB, respectively. Further, assume that their lifetimes are independent. (a) If AA AB = 1/25, how many hours, on average, does the component that lives longer outlive the other component by? (b) If AA 1/25 and AB = 1/20, what is the probability component A outlives component B?
You are given two components, component A and component B, and suppose their lifetimes, in hours, are expo- nential with parameters XA and AB, respectively. Further, assume that their lifetimes are independent. (a) If AA AB = 1/25, how many hours, on average, does the component that lives longer outlive the other component by? (b) If AA 1/25 and AB = 1/20, what is the probability component A outlives component B?
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question

Transcribed Image Text:You are given two components, component A and component B, and suppose their lifetimes, in hours, are expo-
nential with parameters XA and AB, respectively. Further, assume that their lifetimes are independent.
(a) If AA AB = 1/25, how many hours, on average, does the component that lives longer outlive the other
component by?
(b) If AA 1/25 and AB = 1/20, what is the probability component A outlives component B?
Expert Solution
Step 1
According to the provided data,
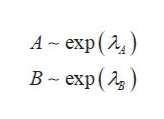
Step 2
a. The concept of memory less property is used here, that is, if X~exp(λ), then P(X>t+s|X>s) = e-dt. Therefore, even elapsing or expanding ‘s’ unit of time X still follows exponential distribution.
So, on average the component that lives longer compare to other component have still an exponential distribution with rate 1/25. The average is,
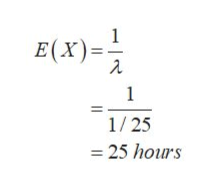
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
