y=F(x) -8-
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:The image displays a graph on a coordinate plane. The graph represents a downward-facing parabola, which is a quadratic function denoted as \( y = F(x) \).
### Detailed Description:
- **Axes:** The graph includes an x-axis (horizontal) and a y-axis (vertical).
- **Scale:** Both axes are marked with a scale displaying integer values, with major grid lines at regular intervals.
- **Graph Characteristics:**
- The parabola opens upwards and appears symmetric around the vertical axis at \( x = 4 \).
- The vertex, or the minimum point, of the parabola is at \( x = 4 \), where the parabola reaches its lowest point.
- The curve intersects the x-axis at \( x = 2 \) and \( x = 6 \), suggesting these are the roots of the equation \( F(x) = 0 \).
- The y-values start at 8, decrease to a minimum of -12, and then increase back to 8, indicating the shape of a parabola.
### Contextual Explanation:
This graph illustrates the basic properties of a quadratic function, showcasing its symmetrical nature and identifiable vertex. Such graphs are common in algebra and pre-calculus courses, where students learn to interpret and construct them based on quadratic equations.
![Decide from the graph whether each limit exists. If a limit exists, estimate its value.
\[ \lim_{x \to 3} F(x) \]
\[ \lim_{x \to 6} F(x) \]
What is the value of the limit? Select the correct choice below and fill in any answer boxes in your choice.
- **A.** \( \lim_{x \to 3} F(x) = \) [______] (Type an integer or a simplified fraction)
- **B.** The limit does not exist.
There is one part remaining.
Click to select and enter your answer(s) and then click Check Answer.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fabbce646-2b21-47d3-ac02-3aed37cd330f%2Fa6dbe5e1-5cea-4afd-8bcb-a7e1f958153a%2Ftcuyfgp_processed.jpeg&w=3840&q=75)
Transcribed Image Text:Decide from the graph whether each limit exists. If a limit exists, estimate its value.
\[ \lim_{x \to 3} F(x) \]
\[ \lim_{x \to 6} F(x) \]
What is the value of the limit? Select the correct choice below and fill in any answer boxes in your choice.
- **A.** \( \lim_{x \to 3} F(x) = \) [______] (Type an integer or a simplified fraction)
- **B.** The limit does not exist.
There is one part remaining.
Click to select and enter your answer(s) and then click Check Answer.
Expert Solution
Step 1
We have to find limit of function F(x) with the help of graph:
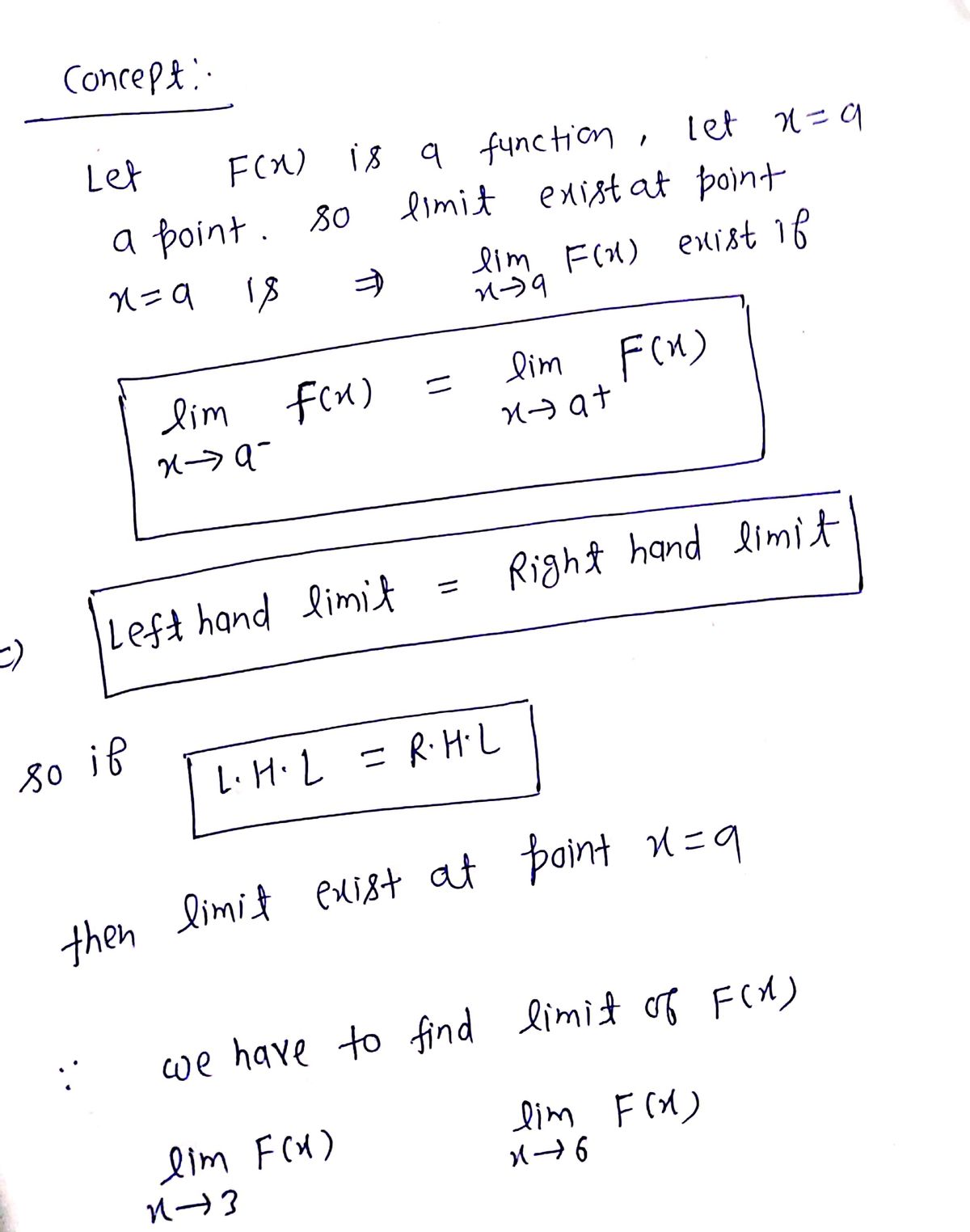
Step by step
Solved in 4 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

