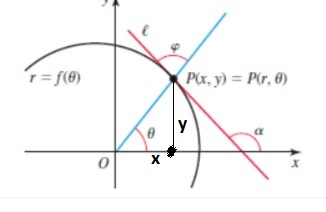
Tangents and normals Let a polar curve be described by r = ƒ(θ), and let ℓ be the line tangent to the curve at the point P(x, y) = P(r, θ) (see figure).
a. Explain why tan a = dy/dx.
b. Explain why tan θ = y/x.
c. Let φ be the angle between ℓ and the line through O and P.
Prove that tan φ = ƒ(θ)/ƒ'(θ).
d. Prove that the values of u for which ℓ is parallel to the x-axis
satisfy tan θ = -ƒ(θ)/ƒ'(θ).
e. Prove that the values of u for which ℓ is parallel to the y-axis
satisfy tan θ = ƒ(θ)/ƒ'(θ).

Consider the given figure:

The line l is tangent to the curve. The tangent line is making alpha angle with the positive x axis. This gives the slope of the line.
The slope of the line is the rate of change of dependent variable with respect to the independent variable.
Therefore, It is said that
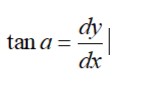
Consider the given figure:
The triangle formed by the point P with the coordinate axis is a right angled triangle.
The tangent of an angle in a triangle is equal to the ratio of perpendicular to the base.
Thus, it is said that
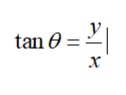
Step by step
Solved in 3 steps with 6 images









