Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
y" - 22y' + 121y = 1) Let C₁ and C₂ be arbitrary constants. The general solution to the related homogeneous differential equation y" - 22y' + 121y = 0 is the function n(x) = C₁ y ₁ (x) + C₂ Y₂ (x) = C₁ +C₂ e-11x 1+x2¹ y(0) = -10, y'(0) = 6. IOTE: The order in which you enter the answers is important; that is, C₁f(x) + C₂g(x) # C₁9(x) + C₂f(x). e-11x 1+x2 is of the form y(x) = y₁(x) u₁(x) + y₂ (x) u₂(x) where u₁(x) = = 2) The particular solution y(x) to the differential equation y" + 22y' + 121y = and u₂(x) = + 3) The most general solution to the non-homogeneous differential equation y" - 22y' + 121y = e-11x 1+x2 dt + is dt

y" - 22y' + 121y = 1) Let C₁ and C₂ be arbitrary constants. The general solution to the related homogeneous differential equation y" - 22y' + 121y = 0 is the function n(x) = C₁ y ₁ (x) + C₂ Y₂ (x) = C₁ +C₂ e-11x 1+x2¹ y(0) = -10, y'(0) = 6. IOTE: The order in which you enter the answers is important; that is, C₁f(x) + C₂g(x) # C₁9(x) + C₂f(x). e-11x 1+x2 is of the form y(x) = y₁(x) u₁(x) + y₂ (x) u₂(x) where u₁(x) = = 2) The particular solution y(x) to the differential equation y" + 22y' + 121y = and u₂(x) = + 3) The most general solution to the non-homogeneous differential equation y" - 22y' + 121y = e-11x 1+x2 dt + is dt

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question

PART 3, PLEASE HIGHLIGHT THE BOXES, BARTLEBY EXPERT ANSWERS ARE WRONG

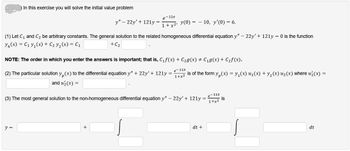
In this exercise you will solve the initial value problem y" 22y' + 121y = -11x e 1 + x²¹ y(0) = − 10, y'(0) = 6. (1) Let C₁ and C₂ be arbitrary constants. The general solution to the related homogeneous differential equation y" - 22y' + 121y = 0 is the function yn(x) = C₁ y₁ (x) + C₂ y₂(x) = C₁ +C₂ y = NOTE: The order in which you enter the answers is important; that is, C₁f(x) + C₂g(x) ‡ C₁9(x) + C₂f(x). (2) The particular solution y(x) to the differential equation y" + 22y' + 121y = is of the form y(x) = y₁(x) u₁(x) + y₂ (x) u₂(x) where u₁(x) 11x 1+x² and u₂(x) = (3) The most general solution to the non-homogeneous differential equation y" - 22y' + 121y = e-11x 1+x2 dt + is dt
Transcribed Image Text:In this exercise you will solve the initial value problem y" 22y' + 121y = -11x e 1 + x²¹ y(0) = − 10, y'(0) = 6. (1) Let C₁ and C₂ be arbitrary constants. The general solution to the related homogeneous differential equation y" - 22y' + 121y = 0 is the function yn(x) = C₁ y₁ (x) + C₂ y₂(x) = C₁ +C₂ y = NOTE: The order in which you enter the answers is important; that is, C₁f(x) + C₂g(x) ‡ C₁9(x) + C₂f(x). (2) The particular solution y(x) to the differential equation y" + 22y' + 121y = is of the form y(x) = y₁(x) u₁(x) + y₂ (x) u₂(x) where u₁(x) 11x 1+x² and u₂(x) = (3) The most general solution to the non-homogeneous differential equation y" - 22y' + 121y = e-11x 1+x2 dt + is dt
Expert Solution
trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question

PART 3, PLEASE HIGHLIGHT THE BOXES, BARTLEBY EXPERT ANSWERS ARE WRONG

In this exercise you will solve the initial value problem y" 22y' + 121y = -11x e 1 + x²¹ y(0) = − 10, y'(0) = 6. (1) Let C₁ and C₂ be arbitrary constants. The general solution to the related homogeneous differential equation y" - 22y' + 121y = 0 is the function yn(x) = C₁ y₁ (x) + C₂ y₂(x) = C₁ +C₂ y = NOTE: The order in which you enter the answers is important; that is, C₁f(x) + C₂g(x) ‡ C₁9(x) + C₂f(x). (2) The particular solution y(x) to the differential equation y" + 22y' + 121y = is of the form y(x) = y₁(x) u₁(x) + y₂ (x) u₂(x) where u₁(x) 11x 1+x² and u₂(x) = (3) The most general solution to the non-homogeneous differential equation y" - 22y' + 121y = e-11x 1+x2 dt + is dt
Transcribed Image Text:In this exercise you will solve the initial value problem y" 22y' + 121y = -11x e 1 + x²¹ y(0) = − 10, y'(0) = 6. (1) Let C₁ and C₂ be arbitrary constants. The general solution to the related homogeneous differential equation y" - 22y' + 121y = 0 is the function yn(x) = C₁ y₁ (x) + C₂ y₂(x) = C₁ +C₂ y = NOTE: The order in which you enter the answers is important; that is, C₁f(x) + C₂g(x) ‡ C₁9(x) + C₂f(x). (2) The particular solution y(x) to the differential equation y" + 22y' + 121y = is of the form y(x) = y₁(x) u₁(x) + y₂ (x) u₂(x) where u₁(x) 11x 1+x² and u₂(x) = (3) The most general solution to the non-homogeneous differential equation y" - 22y' + 121y = e-11x 1+x2 dt + is dt
Solution
Bartleby Expert
SEE SOLUTION
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS