x+y≤9 2x+5y210 x≥0, y 20 D
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
100%

Transcribed Image Text:**Problem 2: Graphical Solution of Inequalities**
Objective: Solve the system of inequalities by graphing and determine if the feasible region is bounded or unbounded.
Inequalities to solve:
1. \( x + y \leq 9 \)
2. \( 2x + 5y \geq 10 \)
3. \( x \geq 0 \)
4. \( y \geq 0 \)
### Graphical Representation
To solve these inequalities graphically:
1. **Graph \( x + y = 9 \):**
- This is a straight line. The region of interest is the area below or on this line.
2. **Graph \( 2x + 5y = 10 \):**
- This is another straight line. The feasible region will be above or on this line.
3. **Graph \( x \geq 0 \) and \( y \geq 0 \):**
- These inequalities ensure that the solution lies in the first quadrant of the coordinate plane.
### Feasible Region
The feasible region is where all these conditions are satisfied simultaneously. It is the intersection of all these shaded areas on the graph.
### Determine if Region is Bounded or Unbounded
- A region is **bounded** if it is enclosed on all sides and forms a closed shape.
- A region is **unbounded** if it extends infinitely in one or more directions.
For this system, examine whether the feasible region satisfies these criteria by interpreting the graph intersection.
This forms the basis of identifying and finding solutions to linear programming problems through graphical methods.
Expert Solution
Step 1
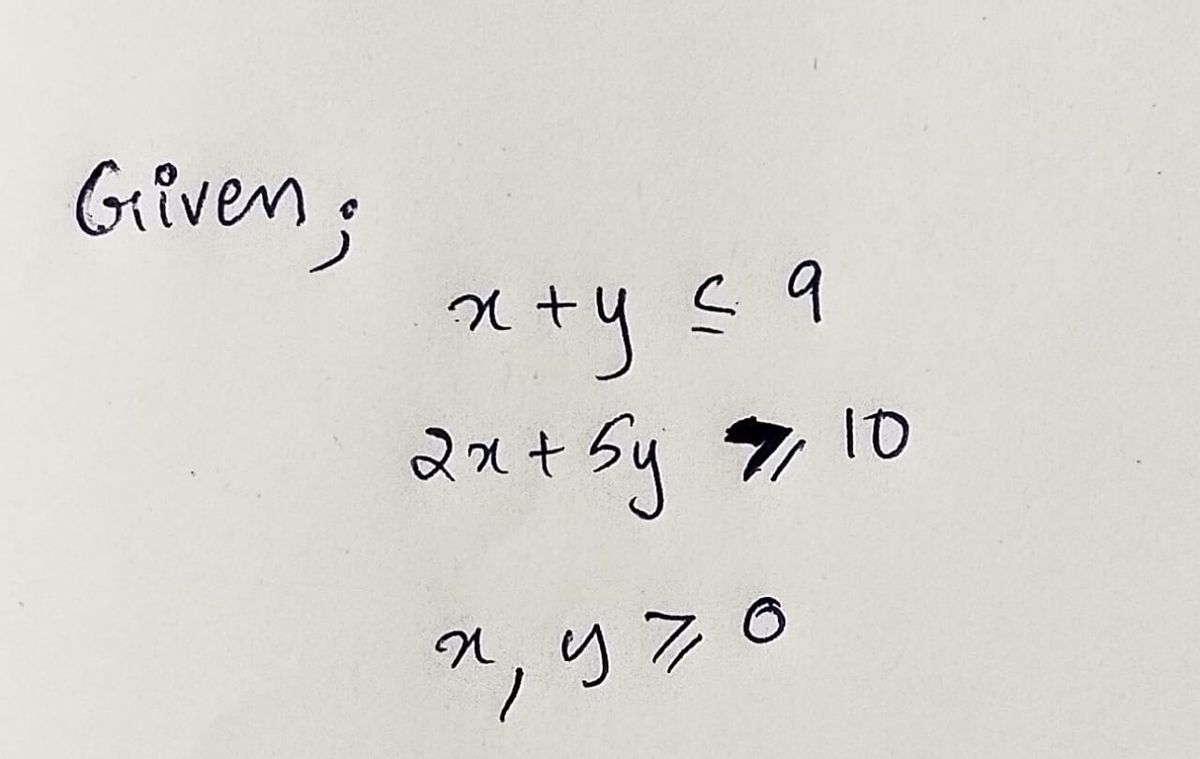
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

