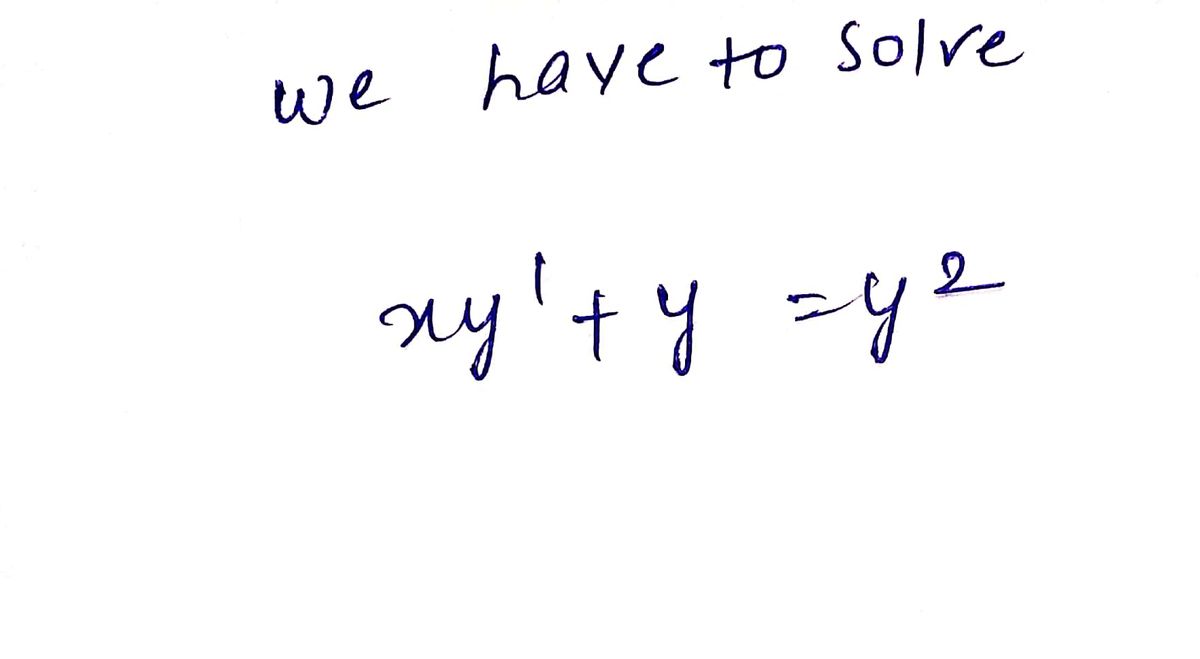1 First-order Odes 2 Second-order Linear Odes 3 Higher Order Linear Odes 4 Systems Of Odes. Phase Plane. Qualitative Methods 5 Series Solutions Of Odes. Special Functions 6 Laplace Transforms 7 Linear Algebra: Matrices, Vectors, Determinants. Linear Systems 8 Linear Algebra: Matrix Eigenvalue Problems 9 Vector Differential Calculus. Grad, Div, Curl 10 Vector Integral Calculus. Integral Theorems 11 Fourier Analysis. Partial Differential Equations (pdes) 12 Partial Differential Equations (pdes) 13 Complex Numbers And Functions 14 Complex Integration 15 Power Series, Taylor Series 16 Laurent Series. Residue Integration 17 Conformal Mapping 18 Complex Analysis And Potential Theory 19 Numerics In General 20 Numeric Linear Algebra 21 Numerics For Odes And Pdes 22 Unconstrauined Optimization. Linear Programming 23 Graphs. Combinatorial Optimization 24 Data Analysis. Probability Theory 25 Mathematical Statistics Chapter2: Second-order Linear Odes
2.1 Homogeneous Linear Odes Of Second Order 2.2 Homogeneous Linear Odes With Constant Coefficients 2.3 Differential Operators 2.4 Modeling Of Free Oscillators Of A Mass-spring System 2.5 Euler-cauchy Equations 2.6 Existence And Uniqueness Of Solutions. Wronskian 2.7 Nonhomogeneous Odes 2.8 Modeling: Forced Oscillations. Resonance 2.9 Modeling: Electric Circuits 2.10 Solution By Variation Of Parameters Chapter Questions Section: Chapter Questions
Problem 1RQ Problem 2RQ Problem 3RQ: By what methods can you get a general solution of a nonhomogeneous ODE from a general solution of a... Problem 4RQ Problem 5RQ Problem 6RQ Problem 7RQ: Find a general solution. Show the details of your calculation.
4y″ + 32y′ + 63y = 0
Problem 8RQ: Find a general solution. Show the details of your calculation.
y″ + y′ − 12y = 0
Problem 9RQ: Find a general solution. Show the details of your calculation.
y″ + 6y′ + 34y = 0
Problem 10RQ: Find a general solution. Show the details of your calculation.
y″ + 0.20y′ + 0.17y = 0
Problem 11RQ: Find a general solution. Show the details of your calculation.
(100D2 − 160D + 64I)y = 0
Problem 12RQ: Find a general solution. Show the details of your calculation.
(D2 + 4πD + 4π2I)y = 0
Problem 13RQ: Find a general solution. Show the details of your calculation.
(x2D2 + 2xD − 12I)y = 0
Problem 14RQ: Find a general solution. Show the details of your calculation.
(x2D2 + xD − 9I)y = 0
Problem 15RQ Problem 16RQ Problem 17RQ Problem 18RQ: Find a general solution. Show the details of your calculation.
yy″ = 2y′2
Problem 19RQ: Solve the problem, showing the details of your work. Sketch or graph the solution.
y″ + 16y =... Problem 20RQ: Solve the problem, showing the details of your work. Sketch or graph the solution.
y″ − 3y′ + 2y =... Problem 21RQ: Solve the problem, showing the details of your work. Sketch or graph the solution.
(x2D2 + xD − I)y... Problem 22RQ: Solve the problem, showing the details of your work. Sketch or graph the solution.
(x2D2 + 15xD +... Problem 23RQ: Find the steady-state current in the RLC-circuit in Fig. 71 when R = 2Ω (2000 Ω), L = 1 H, C = 4 ·... Problem 24RQ: Find a general solution of the homogeneous linear ODE corresponding to the ODE in Prob. 23.
25. Find... Problem 25RQ: Find the steady-state current in the RLC-circuit in Fig. 71 when R = 50 Ω, L = 30 H, C = 0.025 F, E... Problem 26RQ: Find the current in the RLC-circuit in Fig. 71 when R = 40 Ω, L = 0.4 H, C = 10−4 F, E = 220 sin... Problem 27RQ Problem 28RQ Problem 29RQ Problem 30RQ Problem 1RQ
Related questions
Solve the differential equation.
Transcribed Image Text: The equation presented is:
\[ xy' + y = y^2 \]
This is a first-order differential equation, which can be classified as a Bernoulli differential equation because of the presence of \( y^2 \). The term \( y' \) represents the derivative of \( y \) with respect to \( x \).
To solve it, you might use a substitution method. Generally, for a Bernoulli equation of the form \( y' + P(x)y = Q(x)y^n \), you can use the substitution \( v = y^{1-n} \) to transform it into a linear differential equation. For this specific equation, some algebraic manipulation and substitution will be necessary to find the solution.
With integration, one of the major concepts of calculus. Differentiation is the derivative or rate of change of a function with respect to the independent variable.
Expert Solution
Step by step
Solved in 2 steps with 2 images
![The equation presented is:
\[ xy' + y = y^2 \]
This is a first-order differential equation, which can be classified as a Bernoulli differential equation because of the presence of \( y^2 \). The term \( y' \) represents the derivative of \( y \) with respect to \( x \).
To solve it, you might use a substitution method. Generally, for a Bernoulli equation of the form \( y' + P(x)y = Q(x)y^n \), you can use the substitution \( v = y^{1-n} \) to transform it into a linear differential equation. For this specific equation, some algebraic manipulation and substitution will be necessary to find the solution.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F2c222075-437b-48bc-845a-e38a8bd40737%2F684d7712-f7ee-4158-97ec-65dd11337d66%2Fl9jh1l_processed.jpeg&w=3840&q=75)