Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Topic Video
Question
Need help with homework
Determine g’(x)
![**Problem Statement:**
Determine \( g'(x) \) if \( g(x) = \ln \left( \frac{x^2 + 5x + 8}{x^3 + 5x + 8} \right) \).
**Solution Overview:**
To find the derivative \( g'(x) \), we will use the chain rule and the properties of logarithmic differentiation. The function \( g(x) \) is a natural logarithm of a fraction, specifically \( \ln(u(x)) \) where:
\[ u(x) = \frac{x^2 + 5x + 8}{x^3 + 5x + 8} \]
### Steps:
1. **Differentiate the logarithmic function:**
Using the derivative of the natural logarithm, \((\ln(u))' = \frac{1}{u} \cdot u'\).
2. **Apply the quotient rule to find \( u'(x) \):**
For a function \( \frac{f(x)}{h(x)} \), the quotient rule states:
\[
\left(\frac{f}{h}\right)' = \frac{f'h - fh'}{h^2}
\]
3. **Determine \( f(x) = x^2 + 5x + 8 \) and \( h(x) = x^3 + 5x + 8 \):**
- \( f'(x) = 2x + 5 \)
- \( h'(x) = 3x^2 + 5 \)
4. **Apply the quotient rule:**
\[
u'(x) = \frac{(2x + 5)(x^3 + 5x + 8) - (x^2 + 5x + 8)(3x^2 + 5)}{(x^3 + 5x + 8)^2}
\]
5. **Plug \( u \) and \( u' \) into the derivative of the logarithmic function:**
\[
g'(x) = \frac{1}{u(x)} \cdot u'(x)
\]
Simplify this expression for the final result.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F4cbe10c6-7416-4dbe-aac3-86d00105e150%2F2d0f6701-7d56-4e8c-828c-dcbd2388acf5%2Fifw0to_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Determine \( g'(x) \) if \( g(x) = \ln \left( \frac{x^2 + 5x + 8}{x^3 + 5x + 8} \right) \).
**Solution Overview:**
To find the derivative \( g'(x) \), we will use the chain rule and the properties of logarithmic differentiation. The function \( g(x) \) is a natural logarithm of a fraction, specifically \( \ln(u(x)) \) where:
\[ u(x) = \frac{x^2 + 5x + 8}{x^3 + 5x + 8} \]
### Steps:
1. **Differentiate the logarithmic function:**
Using the derivative of the natural logarithm, \((\ln(u))' = \frac{1}{u} \cdot u'\).
2. **Apply the quotient rule to find \( u'(x) \):**
For a function \( \frac{f(x)}{h(x)} \), the quotient rule states:
\[
\left(\frac{f}{h}\right)' = \frac{f'h - fh'}{h^2}
\]
3. **Determine \( f(x) = x^2 + 5x + 8 \) and \( h(x) = x^3 + 5x + 8 \):**
- \( f'(x) = 2x + 5 \)
- \( h'(x) = 3x^2 + 5 \)
4. **Apply the quotient rule:**
\[
u'(x) = \frac{(2x + 5)(x^3 + 5x + 8) - (x^2 + 5x + 8)(3x^2 + 5)}{(x^3 + 5x + 8)^2}
\]
5. **Plug \( u \) and \( u' \) into the derivative of the logarithmic function:**
\[
g'(x) = \frac{1}{u(x)} \cdot u'(x)
\]
Simplify this expression for the final result.
![Below is the transcription of the mathematical derivatives as shown in the image.
Equation 1:
\[ g'(x) = \frac{2x - 5}{x^2 + 5x + 8} - \frac{3x^2 - 5}{x^3 + 5x + 8} \]
Equation 2:
\[ g'(x) = \frac{x^2 + 5x + 8}{2x + 5} - \frac{x^3 + 5x + 8}{3x^2 + 5} \]
Equation 3:
\[ g'(x) = \frac{2x + 5}{x^2 + 5x + 8} + \frac{3x^2 + 5}{x^3 + 5x + 8} \]
There are no graphs or diagrams to explain in this image. The image consists solely of these mathematical expressions.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F4cbe10c6-7416-4dbe-aac3-86d00105e150%2F2d0f6701-7d56-4e8c-828c-dcbd2388acf5%2Ffo68cen_processed.jpeg&w=3840&q=75)
Transcribed Image Text:Below is the transcription of the mathematical derivatives as shown in the image.
Equation 1:
\[ g'(x) = \frac{2x - 5}{x^2 + 5x + 8} - \frac{3x^2 - 5}{x^3 + 5x + 8} \]
Equation 2:
\[ g'(x) = \frac{x^2 + 5x + 8}{2x + 5} - \frac{x^3 + 5x + 8}{3x^2 + 5} \]
Equation 3:
\[ g'(x) = \frac{2x + 5}{x^2 + 5x + 8} + \frac{3x^2 + 5}{x^3 + 5x + 8} \]
There are no graphs or diagrams to explain in this image. The image consists solely of these mathematical expressions.
Expert Solution
Step 1
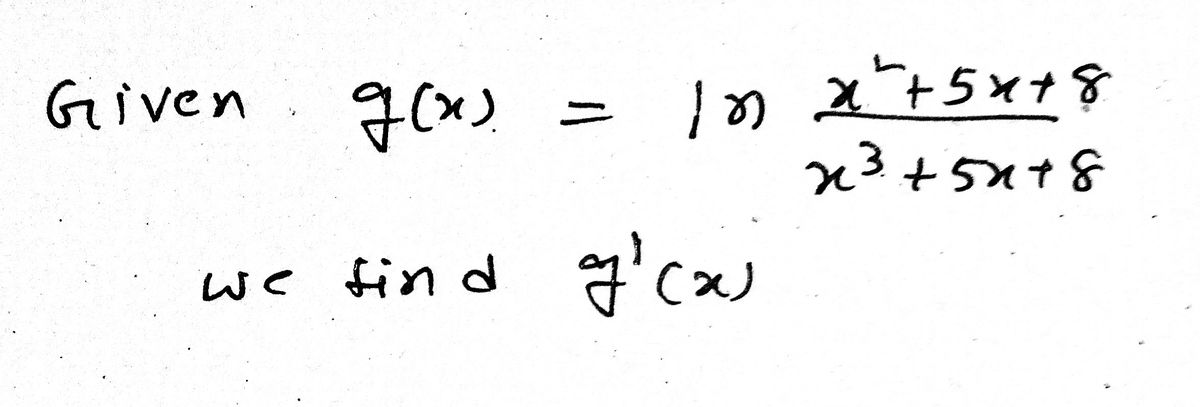
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning