Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
![On this Educational website, we explore the process of finding the indefinite integral of composite functions. Below is a sample problem requiring this technique:
\[ \int x^9 \arccsc(x^{10} + 13) \, dx \]
Here, we are tasked with integrating the function \( x^9 \arccsc(x^{10} + 13) \) with respect to \( x \).
### Key Concepts:
1. **Power Functions:** The integrand includes a power function \( x^9 \), which highlights that understanding the rules of integrating polynomials is vital.
2. **Inverse Trigonometric Functions:** The function \( \arccsc \), the inverse cosecant, is part of the integrand, which may require knowledge of specific integration techniques involving inverse trigonometric functions.
3. **Composite Functions:** Recognizing how to handle composite functions \( x^{10} + 13 \) within the context of integration will be necessary.
### Possible Approach:
To approach this integral, one might consider substitution methods due to the complexity introduced by the \( x^{10} \) term inside the inverse cosecant function.
1. **Substitution:** Let \( u = x^{10} + 13 \). This substitution simplifies the function inside the inverse cosecant.
2. **Differentiation of Substitution:** Compute \( du \). Since \( u = x^{10} + 13 \), \( \frac{du}{dx} = 10x^9 \). This helps to express \( dx \) in terms of \( du \).
This integral demonstrates the multi-step approach often necessary in calculus, combining derivative knowledge with inverse trigonometric and polynomial integration techniques.
### Detailed Explanation:
1. **Perform the Substitution:**
\[
u = x^{10} + 13 \quad \Rightarrow \quad du = 10x^9 dx
\]
Thus, \( dx = \frac{du}{10x^9} \).
2. **Rewrite the Integral in Terms of \( u \):**
\[
\int x^9 \arccsc(u) \cdot \frac{du}{10x^9}
\]
Simplifies to:
\[
\int \frac{1}{10} \arccsc(u) \, du
\]
3. **Evaluate the New Integral:**
\[
\](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fadf70025-15e9-4d93-968e-9d86049b61bd%2F84a04708-ec85-4a50-8a9a-f29e8c2061e6%2Fd1ojr46.jpeg&w=3840&q=75)
Transcribed Image Text:On this Educational website, we explore the process of finding the indefinite integral of composite functions. Below is a sample problem requiring this technique:
\[ \int x^9 \arccsc(x^{10} + 13) \, dx \]
Here, we are tasked with integrating the function \( x^9 \arccsc(x^{10} + 13) \) with respect to \( x \).
### Key Concepts:
1. **Power Functions:** The integrand includes a power function \( x^9 \), which highlights that understanding the rules of integrating polynomials is vital.
2. **Inverse Trigonometric Functions:** The function \( \arccsc \), the inverse cosecant, is part of the integrand, which may require knowledge of specific integration techniques involving inverse trigonometric functions.
3. **Composite Functions:** Recognizing how to handle composite functions \( x^{10} + 13 \) within the context of integration will be necessary.
### Possible Approach:
To approach this integral, one might consider substitution methods due to the complexity introduced by the \( x^{10} \) term inside the inverse cosecant function.
1. **Substitution:** Let \( u = x^{10} + 13 \). This substitution simplifies the function inside the inverse cosecant.
2. **Differentiation of Substitution:** Compute \( du \). Since \( u = x^{10} + 13 \), \( \frac{du}{dx} = 10x^9 \). This helps to express \( dx \) in terms of \( du \).
This integral demonstrates the multi-step approach often necessary in calculus, combining derivative knowledge with inverse trigonometric and polynomial integration techniques.
### Detailed Explanation:
1. **Perform the Substitution:**
\[
u = x^{10} + 13 \quad \Rightarrow \quad du = 10x^9 dx
\]
Thus, \( dx = \frac{du}{10x^9} \).
2. **Rewrite the Integral in Terms of \( u \):**
\[
\int x^9 \arccsc(u) \cdot \frac{du}{10x^9}
\]
Simplifies to:
\[
\int \frac{1}{10} \arccsc(u) \, du
\]
3. **Evaluate the New Integral:**
\[
\
Expert Solution
Step 1
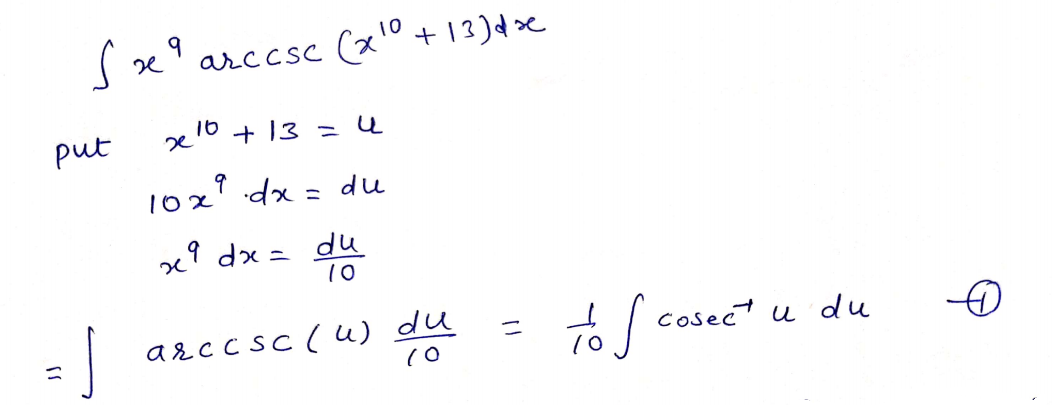
Step 2
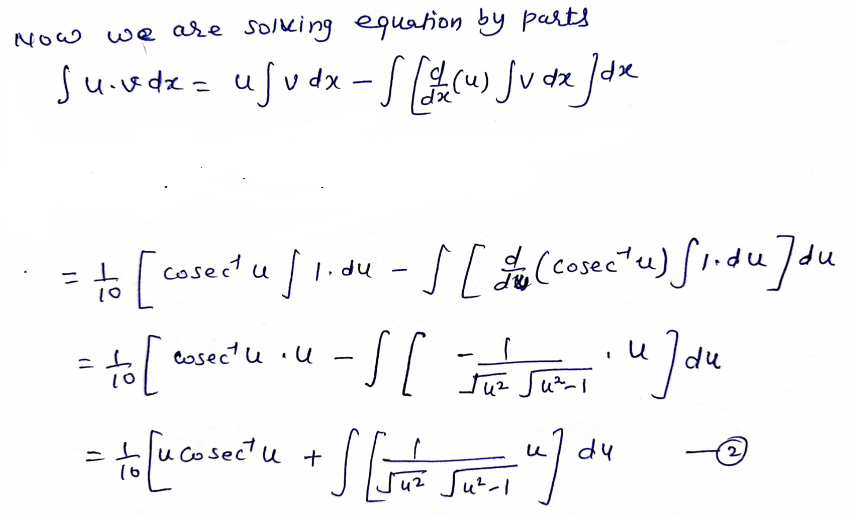
Step by step
Solved in 3 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning