4. Consider a wave equation on an infinite line, J²u 2²u Ա 9 at² əx² = 0. Find the characteristics though the point (1,3). Draw the domains of depen- dence and influence of the point (1,3).
4. Consider a wave equation on an infinite line, J²u 2²u Ա 9 at² əx² = 0. Find the characteristics though the point (1,3). Draw the domains of depen- dence and influence of the point (1,3).
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
100%

Transcribed Image Text:4. Consider a wave equation on an infinite line,
J²u
J²u
9
Ət² əx²
= 0.
=
Find the characteristics though the point (1,3). Draw the domains of depen-
dence and influence of the point (1,3).
Expert Solution
Step 1
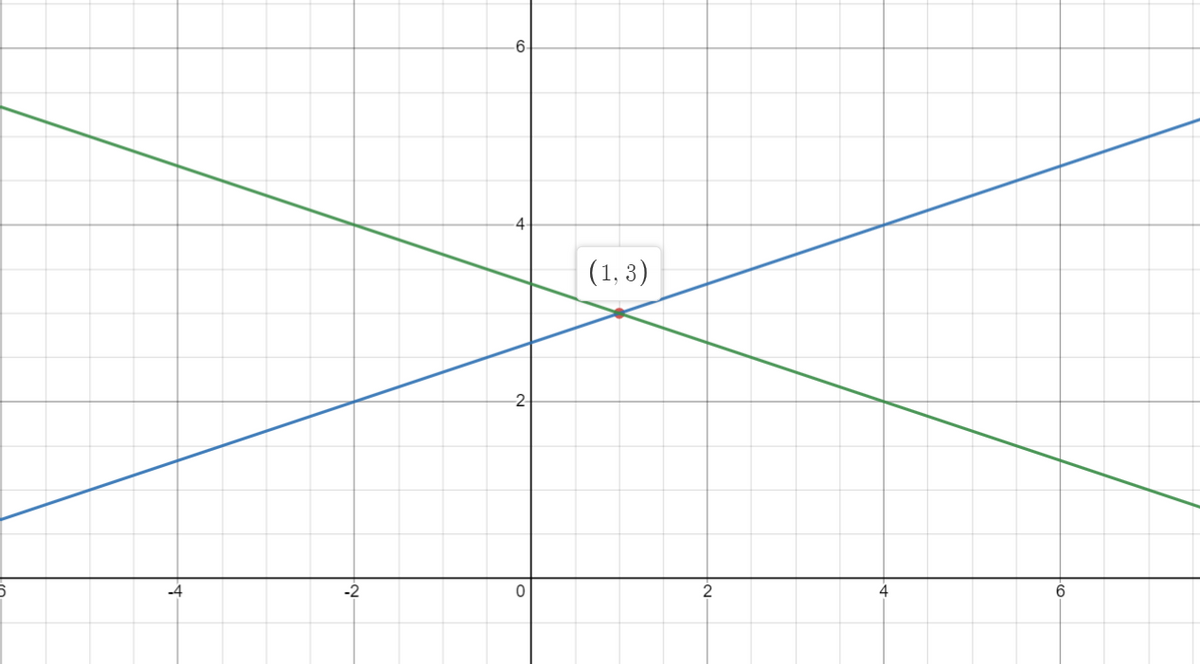
Comparing the given equations with the standard equation , we see that c=3.
Also the point to be analysed is
At the point
The characteristics through the point are given by and .
The lines shown below(green and blue) are the characteristic lines to the given equation.
Step by step
Solved in 3 steps with 3 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
How can you evaluate this equation?
I don't know how to get the interval [-8,10]
![The image displays the following system of equations:
\[ x - 3t = -8 \]
\[ x + 3t = 10 \]
These equations can be solved to find the values of \( x \) and \( t \).
### Steps to Solve:
1. **Add the equations:**
\[
(x - 3t) + (x + 3t) = -8 + 10
\]
Simplifying gives:
\[
2x = 2
\]
2. **Divide by 2 to solve for \( x \):**
\[
x = 1
\]
3. **Substitute \( x = 1 \) back into one of the original equations to solve for \( t \):**
Using the first equation:
\[
1 - 3t = -8
\]
Rearrange to solve for \( t \):
\[
-3t = -8 - 1
\]
\[
-3t = -9
\]
\[
t = 3
\]
### Conclusion:
The solution to the system of equations is \( x = 1 \) and \( t = 3 \).](https://content.bartleby.com/qna-images/question/f003950d-e196-439c-b933-1b2755ea2818/738b180f-f22e-45fe-ba14-fd9d47e1b83d/a55t57m_thumbnail.png)
Transcribed Image Text:The image displays the following system of equations:
\[ x - 3t = -8 \]
\[ x + 3t = 10 \]
These equations can be solved to find the values of \( x \) and \( t \).
### Steps to Solve:
1. **Add the equations:**
\[
(x - 3t) + (x + 3t) = -8 + 10
\]
Simplifying gives:
\[
2x = 2
\]
2. **Divide by 2 to solve for \( x \):**
\[
x = 1
\]
3. **Substitute \( x = 1 \) back into one of the original equations to solve for \( t \):**
Using the first equation:
\[
1 - 3t = -8
\]
Rearrange to solve for \( t \):
\[
-3t = -8 - 1
\]
\[
-3t = -9
\]
\[
t = 3
\]
### Conclusion:
The solution to the system of equations is \( x = 1 \) and \( t = 3 \).
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

