Write out the form of the partial fraction decomposition of the function (as in this example). Do not determine the numerical values of the coefficients.
Write out the form of the partial fraction decomposition of the function (as in this example). Do not determine the numerical values of the coefficients.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Write out the form of the partial fraction decomposition of the function (as in this example). Do not determine the numerical values of the coefficients.
![### Transcription of Mathematical Expression
1. The first mathematical expression is:
\[
\frac{x^6}{x^2 - 4}
\]
This represents a rational function where the numerator is \(x^6\) and the denominator is the difference of squares, specifically, \((x^2 - 4)\).
2. The second part shows a partial fraction decomposition format:
\[
\frac{A}{x-2} + \frac{B}{x+2}
\]
This is used to express the original rational function as a sum of simpler fractions, where \(A\) and \(B\) are constants to be determined.
3. The third expression is:
\[
\frac{x^4}{(x^2 - x + 1)(x^2 + 4)^2}
\]
Here, the numerator is \(x^4\), and the denominator is the product of two factors: a quadratic polynomial \((x^2 - x + 1)\) and the square of another quadratic polynomial \((x^2 + 4)^2\).
### Explanation
- **Expression 1**: The fraction \(\frac{x^6}{x^2 - 4}\) may require simplification using partial fraction decomposition, as indicated by the second format given in Expression 2.
- **Expression 2 (Partial Fractions)**: This form suggests how the original complex fraction might be broken down into simpler components for easier integration or manipulation.
- **Expression 3**: This represents another rational function, involving more complex factors in the denominator, which may also require simplification or decomposition for study in courses related to calculus or algebra.
These expressions are common in advanced algebra, calculus, and mathematical analysis. They help in breaking down complex rational expressions into simpler components for further examination or integration.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F74c7a7c3-55af-48fc-bd21-d0ca6e46b4b9%2F768a9fe2-96ab-4979-ae1e-b895d0e4134c%2Fid1axp_processed.png&w=3840&q=75)
Transcribed Image Text:### Transcription of Mathematical Expression
1. The first mathematical expression is:
\[
\frac{x^6}{x^2 - 4}
\]
This represents a rational function where the numerator is \(x^6\) and the denominator is the difference of squares, specifically, \((x^2 - 4)\).
2. The second part shows a partial fraction decomposition format:
\[
\frac{A}{x-2} + \frac{B}{x+2}
\]
This is used to express the original rational function as a sum of simpler fractions, where \(A\) and \(B\) are constants to be determined.
3. The third expression is:
\[
\frac{x^4}{(x^2 - x + 1)(x^2 + 4)^2}
\]
Here, the numerator is \(x^4\), and the denominator is the product of two factors: a quadratic polynomial \((x^2 - x + 1)\) and the square of another quadratic polynomial \((x^2 + 4)^2\).
### Explanation
- **Expression 1**: The fraction \(\frac{x^6}{x^2 - 4}\) may require simplification using partial fraction decomposition, as indicated by the second format given in Expression 2.
- **Expression 2 (Partial Fractions)**: This form suggests how the original complex fraction might be broken down into simpler components for easier integration or manipulation.
- **Expression 3**: This represents another rational function, involving more complex factors in the denominator, which may also require simplification or decomposition for study in courses related to calculus or algebra.
These expressions are common in advanced algebra, calculus, and mathematical analysis. They help in breaking down complex rational expressions into simpler components for further examination or integration.
Expert Solution
Step 1
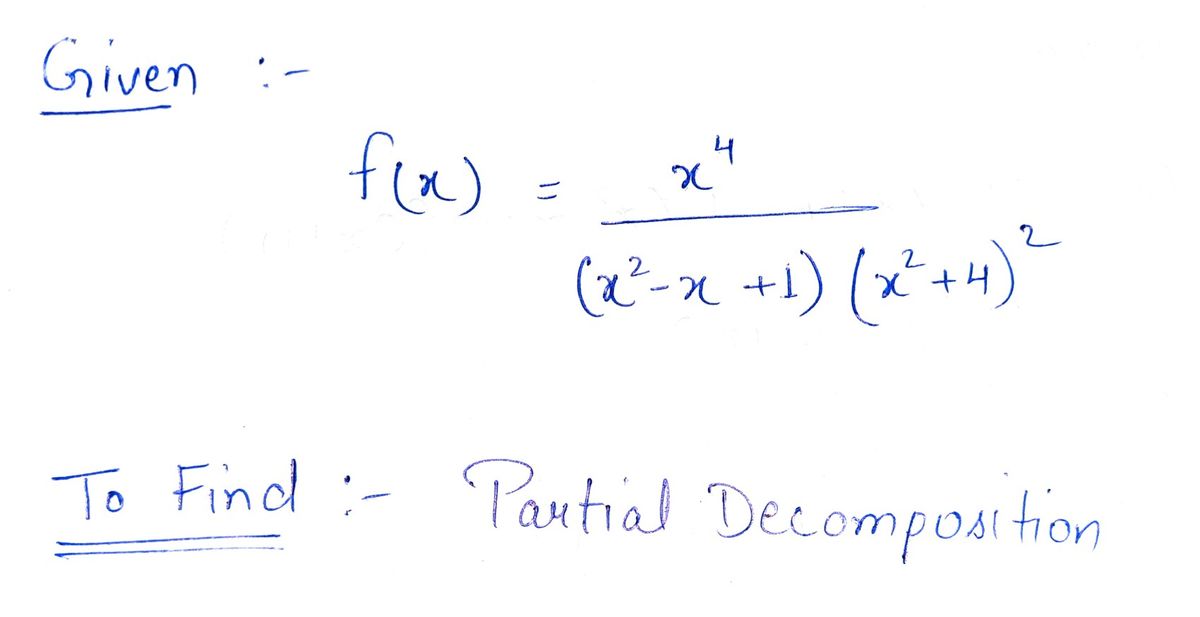
Step by step
Solved in 4 steps with 4 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

