Write a detailed solution to the problem below and upload your answer to Gradescope. Define T: R2 R² by T(x) =T T([22]) = [ 3x1 - 2x2 2x2 X2 • a) Let u = [ U1 = [01] be two vectors in R² and let c be any scalar. Prove and = U2 that T is a linear transformation.
Write a detailed solution to the problem below and upload your answer to Gradescope. Define T: R2 R² by T(x) =T T([22]) = [ 3x1 - 2x2 2x2 X2 • a) Let u = [ U1 = [01] be two vectors in R² and let c be any scalar. Prove and = U2 that T is a linear transformation.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![Write a detailed solution to the problem below and upload your answer to Gradescope.
Define T : R² → R² by T(7) = T ([^]) = [
3x1 2x2
2x2
• a) Let it = [ #] and 8 = [ ] ¹ be two vectors in R² and let c be any scalar. Prove
that T is a linear transformation.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F9c836437-a2a4-49ad-8637-6abf33735fd4%2Fc869f257-182a-4034-b270-709fe2c9203e%2Fpuuhzua_processed.png&w=3840&q=75)
Transcribed Image Text:Write a detailed solution to the problem below and upload your answer to Gradescope.
Define T : R² → R² by T(7) = T ([^]) = [
3x1 2x2
2x2
• a) Let it = [ #] and 8 = [ ] ¹ be two vectors in R² and let c be any scalar. Prove
that T is a linear transformation.
Expert Solution
Step 1
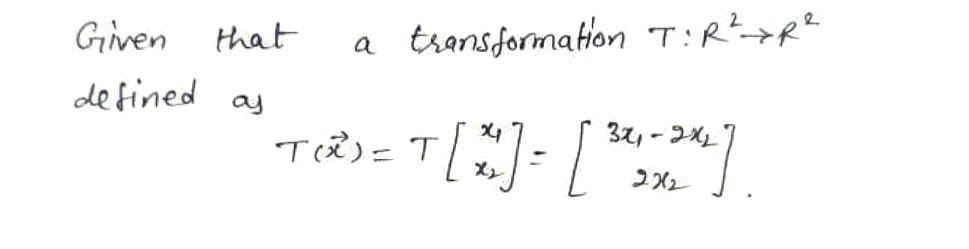
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

