fn = = 2 n²+n−1 3n2-10
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
100%
For each sequence, determine the limit and prove your claim.
Analysis. Please prove using the epsilon method
![The formula depicted in the image is:
\[ f_n = \frac{n^2 + n - 1}{3n^2 - 10} \]
This equation represents a mathematical function \( f_n \) in terms of \( n \). The numerator is \( n^2 + n - 1 \), and the denominator is \( 3n^2 - 10 \). This function can be explored for various values of \( n \) and analyzed to understand its behavior and characteristics.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F3ada9a20-cfc4-4295-96e5-fd4aa8bf1cec%2F8a0fa37f-377b-4242-b1ec-4fe85c5aacd8%2Fvtryo0v_processed.jpeg&w=3840&q=75)
Transcribed Image Text:The formula depicted in the image is:
\[ f_n = \frac{n^2 + n - 1}{3n^2 - 10} \]
This equation represents a mathematical function \( f_n \) in terms of \( n \). The numerator is \( n^2 + n - 1 \), and the denominator is \( 3n^2 - 10 \). This function can be explored for various values of \( n \) and analyzed to understand its behavior and characteristics.
Expert Solution
Step 1: Objective
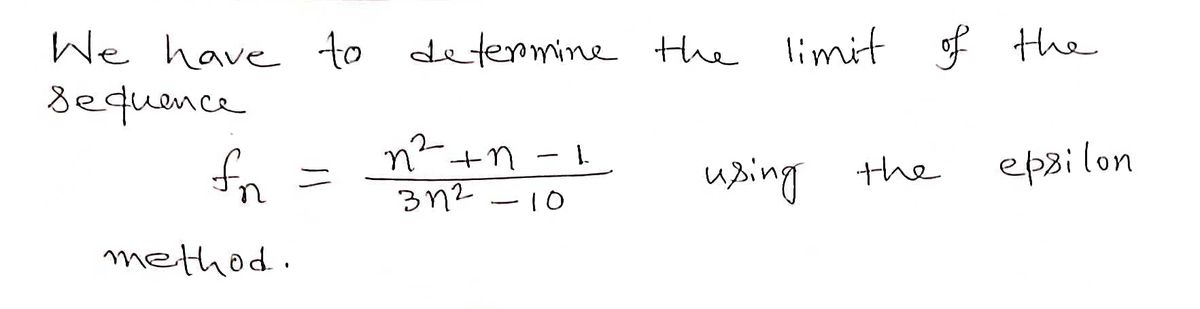
Step by step
Solved in 3 steps with 2 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Hi! Thank you for helping me! Can you please explain why we claim for all n>=3 here?
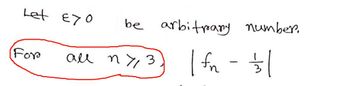
Transcribed Image Text:Let €70
For
be arbitrany number.
| fn
ам пуз
w/-
Solution
Follow-up Question
Why here is < ?
(3n+7)/(9n^2 - 49) should be smaller than (3n+7)/(9n^2 - 30) right?
![The image contains mathematical expressions comparing two rational expressions and performing factorization. Here is the transcription:
1. Starting Expression:
\[
\frac{3n + 7}{9n^2 - 30}
\]
2. Comparison with another expression:
\[
< \frac{3n^2 + 7}{9n^2 - 49}
\]
3. Further simplification of the starting expression:
\[
= \frac{3n + 7}{(3n + 7)(3n - 7)}
\]
The red circle highlights the comparison between the initial expression and the expression to which it is being compared. The inequality symbol "<" indicates that the first expression is less than the second.
Explanation of Simplification:
- The denominator \(9n^2 - 49\) in the second expression is a difference of squares, which can be factored as \((3n + 7)(3n - 7)\).
- The denominator of the initial expression \(9n^2 - 30\) is not factored in the transcription.
This transcription helps illustrate algebraic manipulation through comparison and simplification of rational expressions.](https://content.bartleby.com/qna-images/question/3ada9a20-cfc4-4295-96e5-fd4aa8bf1cec/af498217-9746-4d72-9bed-165d70955c0f/qsasut6_thumbnail.png)
Transcribed Image Text:The image contains mathematical expressions comparing two rational expressions and performing factorization. Here is the transcription:
1. Starting Expression:
\[
\frac{3n + 7}{9n^2 - 30}
\]
2. Comparison with another expression:
\[
< \frac{3n^2 + 7}{9n^2 - 49}
\]
3. Further simplification of the starting expression:
\[
= \frac{3n + 7}{(3n + 7)(3n - 7)}
\]
The red circle highlights the comparison between the initial expression and the expression to which it is being compared. The inequality symbol "<" indicates that the first expression is less than the second.
Explanation of Simplification:
- The denominator \(9n^2 - 49\) in the second expression is a difference of squares, which can be factored as \((3n + 7)(3n - 7)\).
- The denominator of the initial expression \(9n^2 - 30\) is not factored in the transcription.
This transcription helps illustrate algebraic manipulation through comparison and simplification of rational expressions.
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

