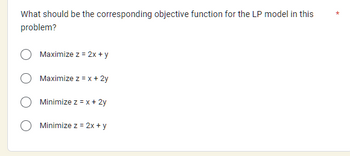
Axis is an aspiring freshman at Saint Louis University. He realizes that “all study and no play make Axis a dull boy.” As a result, Axis wants to apportion his available time of about 10 hours a day between study and play. He estimates that play is twice as much fun as study. He also wants to study at least as much as he plays. However, Axis realizes that if he is going to get all his homework done, he cannot play more than 4 hours a day. With the use of Linear Programming (LP), help Axis allocate his time to maximize his pleasure from both study and play. 1. What should be the corresponding objective function for the LP model in this problem and the complete set of constraints? 2. Graph and identify how many corner points are there and which provides optimal solution to the problem
Unitary Method
The word “unitary” comes from the word “unit”, which means a single and complete entity. In this method, we find the value of a unit product from the given number of products, and then we solve for the other number of products.
Speed, Time, and Distance
Imagine you and 3 of your friends are planning to go to the playground at 6 in the evening. Your house is one mile away from the playground and one of your friends named Jim must start at 5 pm to reach the playground by walk. The other two friends are 3 miles away.
Profit and Loss
The amount earned or lost on the sale of one or more items is referred to as the profit or loss on that item.
Units and Measurements
Measurements and comparisons are the foundation of science and engineering. We, therefore, need rules that tell us how things are measured and compared. For these measurements and comparisons, we perform certain experiments, and we will need the experiments to set up the devices.
Axis is an aspiring freshman at Saint Louis University. He realizes that “all study and no play make Axis a dull boy.” As a result, Axis wants to apportion his available time of about 10 hours a day between study and play. He estimates that play is twice as much fun as study. He also wants to study at least as much as he plays. However, Axis realizes that if he is going to get all his homework done, he cannot play more than 4 hours a day. With the use of Linear Programming (LP), help Axis allocate his time to maximize his pleasure from both study and play.
1. What should be the corresponding objective function for the LP model in this problem and the complete set of constraints?
2. Graph and identify how many corner points are there and which provides optimal solution to the problem
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images