Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Topic Video
Question

Transcribed Image Text:### Problem Statement
What is the smallest positive solution to \(5\sin^2 x - \cos^2 x = 1\)? Round to 2 decimal places.
---
### Explanation
This problem involves solving a trigonometric equation to find the smallest positive solution for \(x\). The equation combines both sine and cosine functions, and solving it typically involves using trigonometric identities and algebraic manipulation.
1. **Trigonometric Identity:** One key identity that might be useful is \(\sin^2 x + \cos^2 x = 1\).
2. **Algebraic Manipulation:** You may try expressing the equation in terms of a single trigonometric function, using the identity mentioned above to simplify \(\cos^2 x\).
3. **Potential Method of Solution:**
- Substitute \(\cos^2 x\) with \(1 - \sin^2 x\).
- Solve the resulting quadratic equation in terms of \(\sin x\).
- Find the smallest positive solution for \(x\).
This exercise is a practice of combining knowledge of trigonometry with algebraic techniques to find a specific numerical solution.
Expert Solution
Step 1
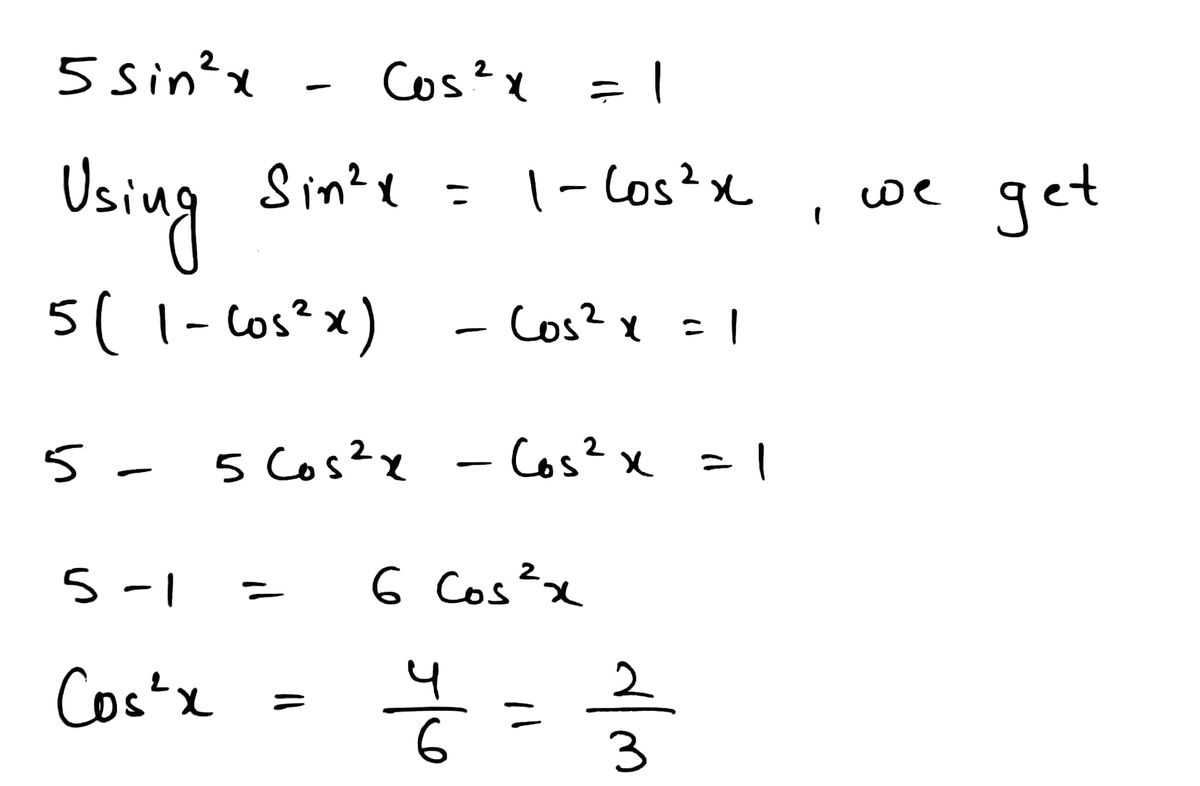
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning