We want to find functions u₁(x) and u₂(x) such that yp = U₁Y₁+U₂Y₂ is a particular solution. We can find the derivatives of these functions as follows. W U₁ = = -e-2x(2 + ex)-1 -e-3x W₂ e-x(2 + ex)-1 -e-3x
We want to find functions u₁(x) and u₂(x) such that yp = U₁Y₁+U₂Y₂ is a particular solution. We can find the derivatives of these functions as follows. W U₁ = = -e-2x(2 + ex)-1 -e-3x W₂ e-x(2 + ex)-1 -e-3x
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter5: Inverse, Exponential, And Logarithmic Functions
Section: Chapter Questions
Problem 18T
Related questions
Question

Transcribed Image Text:We have found the following Wronskians.
W = -e-³x; W₁ = -
We want to find functions u₁(x) and u₂(x) such that yp = U₁Y₁ + U₂y₂ is a particular solution. We can find the derivatives of these functions as follows.
W
=
1
W
-e-2x(2 + ex)-1
-e-3x
-e-²x(2 + ex)-¹; W₂ = e¯x(2 + ex)-¹
W₂
W
ex(2 + ex)-1
-e-3x
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 3 steps

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
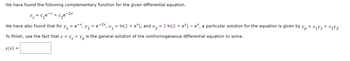
Transcribed Image Text:We have found the following complementary function for the given differential equation.
Y=₁₂x+
c₂e-2x
We have also found that for y₁ = ex, y₂ = e-²x, ‚ U₁ = In(2 + e*), and U₂ = 2 In(2 + e*) – e*, a particular solution for the equation is given by y₁ = U₁Y₁+U₂Y₂
To finish, use the fact that y = y + y is the general solution of the nonhomogeneous differential equation to solve.
y(x) =
Solution
Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,