Homework Help is Here – Start Your Trial Now!
Math
Calculus
Evaluate the integral. Step 1 dx 62 (7²-11³/2

Evaluate the integral. Step 1 dx 62 (7²-11³/2

Calculus: Early Transcendentals
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
See similar textbooks
icon
Related questions
Question
100%

please help i'm having trouble

### Step 3 So far we have the following: \[ \int_{\frac{\pi}{3}}^{\sec^{-1}(8)} \left( \frac{\cos(\theta)}{\sin^2(\theta)} \right) d\theta \] We can now use the substitution \( u = \sin(\theta) \), so \( du = \boxed{\cos(\theta)} \checkmark \, d\theta \). Once more, we must also make a substitution for the limits of integration. When \( \theta = \frac{\pi}{3} \), \( u = \boxed{1} \red{\red{\text{x}}} \). Further, when \[ \theta = \sec^{-1}(8), \, u = \boxed{- \frac{1}{\sin(\theta)}} \red{\red{\text{x}}}. \]
Transcribed Image Text:### Step 3 So far we have the following: \[ \int_{\frac{\pi}{3}}^{\sec^{-1}(8)} \left( \frac{\cos(\theta)}{\sin^2(\theta)} \right) d\theta \] We can now use the substitution \( u = \sin(\theta) \), so \( du = \boxed{\cos(\theta)} \checkmark \, d\theta \). Once more, we must also make a substitution for the limits of integration. When \( \theta = \frac{\pi}{3} \), \( u = \boxed{1} \red{\red{\text{x}}} \). Further, when \[ \theta = \sec^{-1}(8), \, u = \boxed{- \frac{1}{\sin(\theta)}} \red{\red{\text{x}}}. \]
--- ### Evaluate the Integral \[ \int_{2}^{8} \frac{dx}{(x^2 - 1)^{3/2}} \] --- #### Step 1 Recall the Inverse Substitution Rule, where \(f\) and \(g\) are differentiable functions and \(g\) is one-to-one. \[ \int f(x)dx = \int f(g(t))g'(t) \, dt \] We are given the following: \[ \int_{2}^{8} \frac{dx}{(x^2 - 1)^{3/2}} \] We note that \((x^2 - 1)^{3/2} = \left(\sqrt{x^2 - 1}\right)^3\). Therefore, the following entry from the Table of Trigonometric Substitutions is appropriate. \[ \begin{array}{|c|c|c|} \hline \text{Expression} & \text{Substitution} & \text{Identity} \\ \hline \sqrt{x^2 - a^2} & x = a \sec(\theta), \quad 0 \leq \theta < \frac{\pi}{2} \quad \text{or} \quad \frac{\pi}{2} \leq \theta < \frac{3\pi}{2} & \sec^2(\theta) - 1 = \tan^2(\theta) \\ \hline \end{array} \] If \( \left(\sqrt{x^2 - 1}\right)^3 = \left(\sqrt{x^2 - a^2}\right)^3 \), then \(a = 1\). Therefore, we can let \( x = \sec(\theta) \), so \(dx = \left(\sec(\theta)\tan(\theta)\right) \, d\theta\). We also must make a substitution for the limits of integration in the definite integral. Since \( x = \sec(\theta) \), we note that when \( x = 2 \), \( \theta = \sec^{-1}(2) = \frac{\pi}{3}\). Furthermore, when \( x = 8 \), \( \theta = \sec^{-1}(8) \). --- #### Step 2 We have determined that if we
Transcribed Image Text:--- ### Evaluate the Integral \[ \int_{2}^{8} \frac{dx}{(x^2 - 1)^{3/2}} \] --- #### Step 1 Recall the Inverse Substitution Rule, where \(f\) and \(g\) are differentiable functions and \(g\) is one-to-one. \[ \int f(x)dx = \int f(g(t))g'(t) \, dt \] We are given the following: \[ \int_{2}^{8} \frac{dx}{(x^2 - 1)^{3/2}} \] We note that \((x^2 - 1)^{3/2} = \left(\sqrt{x^2 - 1}\right)^3\). Therefore, the following entry from the Table of Trigonometric Substitutions is appropriate. \[ \begin{array}{|c|c|c|} \hline \text{Expression} & \text{Substitution} & \text{Identity} \\ \hline \sqrt{x^2 - a^2} & x = a \sec(\theta), \quad 0 \leq \theta < \frac{\pi}{2} \quad \text{or} \quad \frac{\pi}{2} \leq \theta < \frac{3\pi}{2} & \sec^2(\theta) - 1 = \tan^2(\theta) \\ \hline \end{array} \] If \( \left(\sqrt{x^2 - 1}\right)^3 = \left(\sqrt{x^2 - a^2}\right)^3 \), then \(a = 1\). Therefore, we can let \( x = \sec(\theta) \), so \(dx = \left(\sec(\theta)\tan(\theta)\right) \, d\theta\). We also must make a substitution for the limits of integration in the definite integral. Since \( x = \sec(\theta) \), we note that when \( x = 2 \), \( \theta = \sec^{-1}(2) = \frac{\pi}{3}\). Furthermore, when \( x = 8 \), \( \theta = \sec^{-1}(8) \). --- #### Step 2 We have determined that if we
Expert Solution
trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 5 steps with 5 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
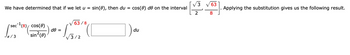
We have determined that if we let u = sin(0), then du sec-¹ (8) cos(0) sin²(0) [sec=² (8) Jπ/3 de = 63/8 √√3/2 cos(0) de on the interval du /3 2 -/ 63 8 Applying the substitution gives us the following result.
Transcribed Image Text:We have determined that if we let u = sin(0), then du sec-¹ (8) cos(0) sin²(0) [sec=² (8) Jπ/3 de = 63/8 √√3/2 cos(0) de on the interval du /3 2 -/ 63 8 Applying the substitution gives us the following result.
Solution
Bartleby Expert
SEE SOLUTION
Recommended textbooks for you
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning
Thomas' Calculus (14th Edition)
Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman
Precalculus
Precalculus
Calculus
ISBN:
9780135189405
Author:
Michael Sullivan
Publisher:
PEARSON
Calculus: Early Transcendental Functions
Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning
SEE MORE TEXTBOOKS