I da By making the linear transformation 21 = y₁ ay2, 22 = 2y1 + y2 S[y1, y2] = = dx [y² + 2y2 + (2y1 + y2)²].
I da By making the linear transformation 21 = y₁ ay2, 22 = 2y1 + y2 S[y1, y2] = = dx [y² + 2y2 + (2y1 + y2)²].
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
100%
![S[y₁, 92] = [ dx [y² + 2y/² + (2y1 + y2)²].
By making the linear transformation
21 = y₁ + ay2, 22 = 2y1 + y2
*
Find the general solution of the Euler-Lagrange equations for (2₁, 22),
and hence find the general solution for (y₁,Y2).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F59d44c96-efb1-4f3c-83b3-5a6a84cf94cb%2F1029576b-fc84-4147-8187-4d0a77c91797%2F2dvv3jr_processed.jpeg&w=3840&q=75)
Transcribed Image Text:S[y₁, 92] = [ dx [y² + 2y/² + (2y1 + y2)²].
By making the linear transformation
21 = y₁ + ay2, 22 = 2y1 + y2
*
Find the general solution of the Euler-Lagrange equations for (2₁, 22),
and hence find the general solution for (y₁,Y2).
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step 1: Write the given functional integration
VIEWStep 2: Use the given linear transformation
VIEWStep 3: Write the Euler Lagrange equations for z1,z2
VIEWStep 4: Find a second order homogeneous linear differential equation for z2
VIEWStep 5: Determine the solutions of the Euler Lagrange equations for (z1,z2)
VIEWStep 6: Determine the general solution for (y1,y2)
VIEWSolution
VIEWStep by step
Solved in 7 steps with 7 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
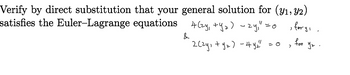
Transcribed Image Text:Verify by direct substitution that your general solution for (y₁, Y2)
satisfies the Euler-Lagrange equations 4(zy, +₂) - zy₁" = 0 for y₁
)
&
2 (²y₁ + y₂) - 4 y₂²" = 0
>
for
y₂.
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

