Verfy that each of the funcions € ³ √ m² en ² Ulinn (x14₁3) = ē sates frer Laplace's any as my equation N U (2₁9,3) = 2 U₂ (41413) nzl Satisfies the same smnx m = 0, 1, 2₁ -- Uxx+lay +llzz = 0 and the boundary conditions Uco, y₁ 8) = U (1T₁, 4₁ 3) = 0, Uly (2₁0, 8) = lly (2,₁11, 3) = 0 Show itwat linear combination -) n=1₁2₁- -. differential equation and boundary conditions.
Verfy that each of the funcions € ³ √ m² en ² Ulinn (x14₁3) = ē sates frer Laplace's any as my equation N U (2₁9,3) = 2 U₂ (41413) nzl Satisfies the same smnx m = 0, 1, 2₁ -- Uxx+lay +llzz = 0 and the boundary conditions Uco, y₁ 8) = U (1T₁, 4₁ 3) = 0, Uly (2₁0, 8) = lly (2,₁11, 3) = 0 Show itwat linear combination -) n=1₁2₁- -. differential equation and boundary conditions.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
#0016
Please show all the steps
![### Verification of Functions in Laplace's Equation
We aim to verify that each of the following functions:
\[ U_{mn}(x, y, z) = e^{-z \sqrt{m^2 + n^2}} \cos my \sin nx \]
where \( m = 0, 1, 2, \ldots \) and \( n = 1, 2, \ldots \),
satisfies Laplace's equation:
\[ U_{xx} + U_{yy} + U_{zz} = 0 \]
and the boundary conditions:
\[ U(0, y, z) = U(\pi, y, z) = 0, \]
\[ U_y(x, 0, z) = U_y(x, \pi, z) = 0 \]
We also show that any linear combination:
\[ U(x, y, z) = \sum_{n=1}^{N} U_n(x, y, z) \]
satisfies the same differential equation and boundary conditions.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F9c55fd55-ae67-4b97-a36c-91359ff73a6f%2F95db963d-92d0-4007-a377-2db02fa0d1f1%2F7dz5jfj_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### Verification of Functions in Laplace's Equation
We aim to verify that each of the following functions:
\[ U_{mn}(x, y, z) = e^{-z \sqrt{m^2 + n^2}} \cos my \sin nx \]
where \( m = 0, 1, 2, \ldots \) and \( n = 1, 2, \ldots \),
satisfies Laplace's equation:
\[ U_{xx} + U_{yy} + U_{zz} = 0 \]
and the boundary conditions:
\[ U(0, y, z) = U(\pi, y, z) = 0, \]
\[ U_y(x, 0, z) = U_y(x, \pi, z) = 0 \]
We also show that any linear combination:
\[ U(x, y, z) = \sum_{n=1}^{N} U_n(x, y, z) \]
satisfies the same differential equation and boundary conditions.
Expert Solution
Step 1
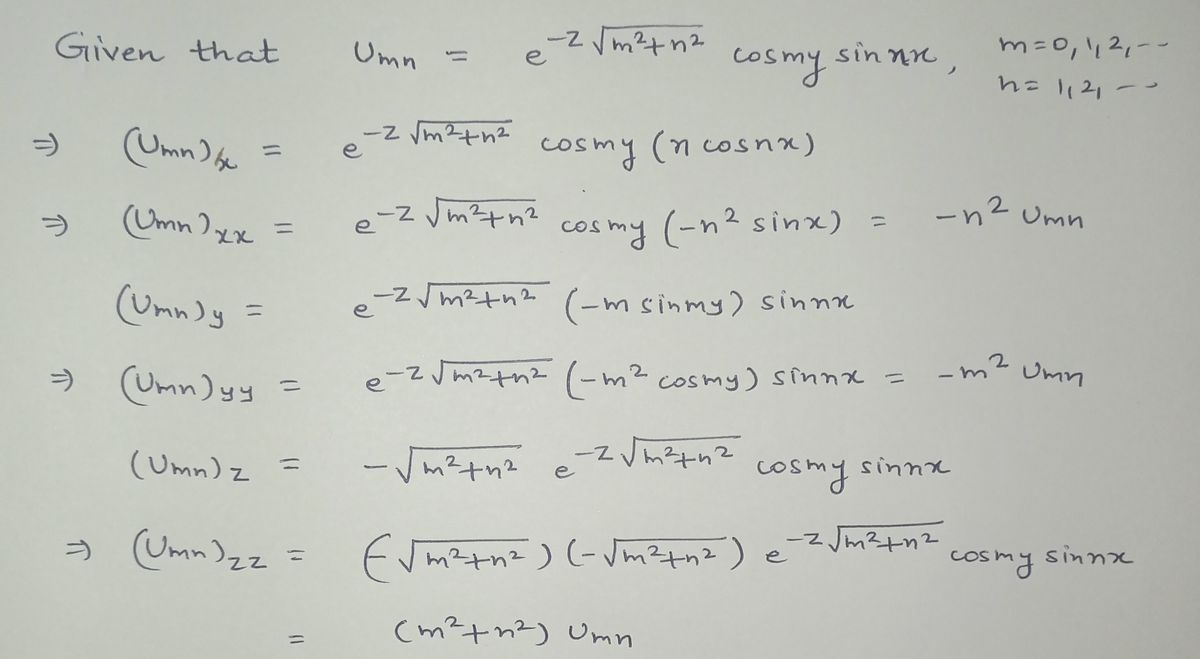
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

