V (o)=0 VG) If B=0 = • Asin Bix VG-C)=√₁₂ = V₂ - Asin BL Asin BL A = -√₂ Sinßl Ta=jV₂ Prove -j Vs Ces Bx Z₂ Sinße
V (o)=0 VG) If B=0 = • Asin Bix VG-C)=√₁₂ = V₂ - Asin BL Asin BL A = -√₂ Sinßl Ta=jV₂ Prove -j Vs Ces Bx Z₂ Sinße
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:**Transcription of Handwritten Notes for Educational Use**
### Context
These notes pertain to the analysis of a voltage function \( V(x) \) and its implications in a given scenario. The mathematical expressions suggest a focus on wave or signal analysis, possibly within the field of electrical engineering or physics.
### Detailed Transcription
- **Condition and Implications**
- If \( V(0) = 0 \), then it implies that \( B = 0 \).
- **Expression for Voltage**
- \( V(x) = A \sin \beta x \)
- At x = L:
- \( V(L) = V_s = -A \sin \beta L \)
- From this equation, it follows that:
- \( A = \frac{V_s}{\sin \beta L} \)
- **Proof**
- The goal is to prove the expression:
- \( I(x) = -i \frac{V_s \cos \beta x}{Z_0 \sin \beta L} \)
### Explanation
- **Variables and Parameters**
- \( V(x) \) represents the voltage as a function of position \( x \).
- \( A \) and \( B \) are constants related to the amplitude of the wave.
- \( \beta \) is likely the propagation constant.
- \( V_s \) denotes the voltage at the position \( x = L \).
- \( Z_0 \) represents the characteristic impedance.
- \( I(x) \) is the current related to \( x \).
### Note
These equations are often encountered in the study of transmission lines or in the analysis of sinusoidal steady-state responses in circuits. Understanding the boundary conditions and the resultant expressions is crucial for validating the behavior of electrical signals over a medium.
![The image contains a mathematical derivation related to electrical circuits, specifically discussing current \( I(x) \). Below is the transcription and explanation of the content:
### Transcription:
\[ I(x) = - \frac{1}{Z} \frac{dV}{dx} = -\frac{1}{j\omega L} [A \beta \cos \beta x - B \beta \sin \beta x] \]
\[ -\frac{1}{j} = j \]
\[ \omega^2 LC = 1 \]
\[ I(x) = \frac{j}{Z_0} (A \cos \beta x - B \sin \beta x) \]
\[ \sqrt{\frac{V_C}{V_C}} \]
### Explanation of Diagram:
The diagram illustrates a transmission line with various parameters:
- It is labeled with the voltage \( V(x) \) and distance \( x \).
- The transmission line is represented by a rectangular shape, aligned horizontally, with \( x = 0 \) on one end and \( x = -l \) on the other. The arrow indicates the direction of increasing \( x \).
- The diagram and equations suggest that this is part of an analysis of wave propagation or signal transmission in a linear medium, incorporating parameters such as impedance \( Z \) and characteristics of the medium defined by \( \omega, L, \) and \( C \).
This content appears to be part of an advanced lesson on transmission lines in the context of electrical engineering or physics, focusing on wave equations and impedance matching.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F3af11e6a-2a61-4302-a4ee-f3c4efdfe331%2F5d1ad1e1-70f1-464d-a6a9-80e11d4955f7%2F7tbjx3t_processed.jpeg&w=3840&q=75)
Transcribed Image Text:The image contains a mathematical derivation related to electrical circuits, specifically discussing current \( I(x) \). Below is the transcription and explanation of the content:
### Transcription:
\[ I(x) = - \frac{1}{Z} \frac{dV}{dx} = -\frac{1}{j\omega L} [A \beta \cos \beta x - B \beta \sin \beta x] \]
\[ -\frac{1}{j} = j \]
\[ \omega^2 LC = 1 \]
\[ I(x) = \frac{j}{Z_0} (A \cos \beta x - B \sin \beta x) \]
\[ \sqrt{\frac{V_C}{V_C}} \]
### Explanation of Diagram:
The diagram illustrates a transmission line with various parameters:
- It is labeled with the voltage \( V(x) \) and distance \( x \).
- The transmission line is represented by a rectangular shape, aligned horizontally, with \( x = 0 \) on one end and \( x = -l \) on the other. The arrow indicates the direction of increasing \( x \).
- The diagram and equations suggest that this is part of an analysis of wave propagation or signal transmission in a linear medium, incorporating parameters such as impedance \( Z \) and characteristics of the medium defined by \( \omega, L, \) and \( C \).
This content appears to be part of an advanced lesson on transmission lines in the context of electrical engineering or physics, focusing on wave equations and impedance matching.
Expert Solution
Step 1
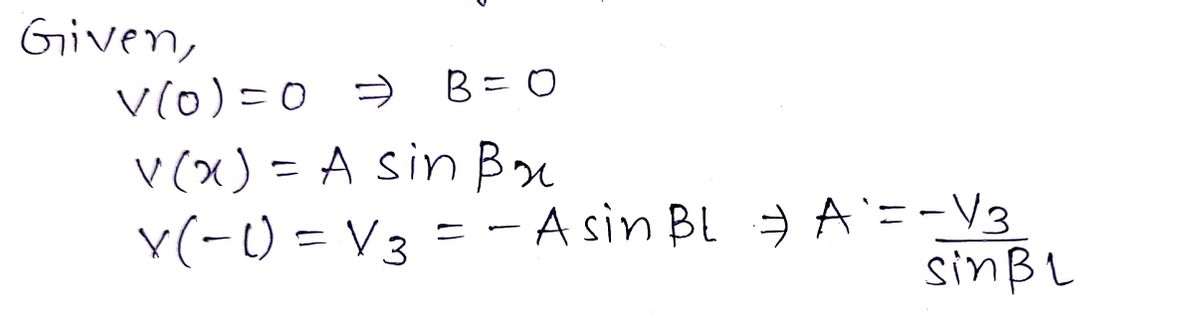
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

