Using the laws of boolean algebra simplify these expressions and list the law(s) used to justify each step. And show a truth table for the original expression and verify that your final expression satisfies the same truth table. a. A' + A'B'CD' + A'B'C'D' + AB'C' + AB'CD' + ABD + BC'D b. A'B' + A'BC' + (A + C')'
Using the laws of boolean algebra simplify these expressions and list the law(s) used to justify each step. And show a truth table for the original expression and verify that your final expression satisfies the same truth table.
a. A' + A'B'CD' + A'B'C'D' + AB'C' + AB'CD' + ABD + BC'D
b. A'B' + A'BC' + (A + C')'
(a.)
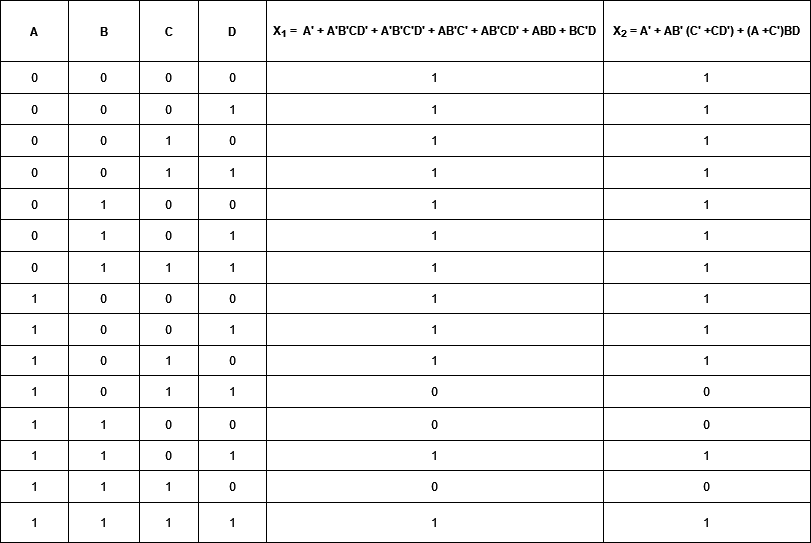
F1 = A' + A'B'CD' + A'B'C'D' + AB'C' + AB'CD' + ABD + BC'D
= A'(1 + B'CD' +B'C'D') + AB' (C' +CD') + (A +C')BD .........(i)
We know that: X + 1 = 1 (Dominant Law)
Therefore, (1 + B'CD' +B'C'D') = 1
So our function become,
F1 = A' + AB' (C' +CD') + (A +C')BD ..........(ii)
Now let us assume original fuction as X1 and reduced function as X2
X1 = A' + A'B'CD' + A'B'C'D' + AB'C' + AB'CD' + ABD + BC'D
& X2 = A' + AB' (C' +CD') + (A +C')BD
Truth Table:
Step by step
Solved in 3 steps with 2 images









