Using the 2-factor approximation algorithm for euclidean-TSP that we discussed, find the distance of the tour starting from and ending in Pensacola. Use the following table to work out the graph and answer, using Kruskall's algorithm. Pensacola Tallahassee Miami Jacksonville Orlando Pensacola 10 196 670 355 461 Tallahassee 196 0 479 164 270 Miami 670 479 10 350 228 Jacksonville 355 164 350 0 163 Orlando 461 270 228 163 0
Please be as detailed as possible

The graph for given adjacency matrix will be
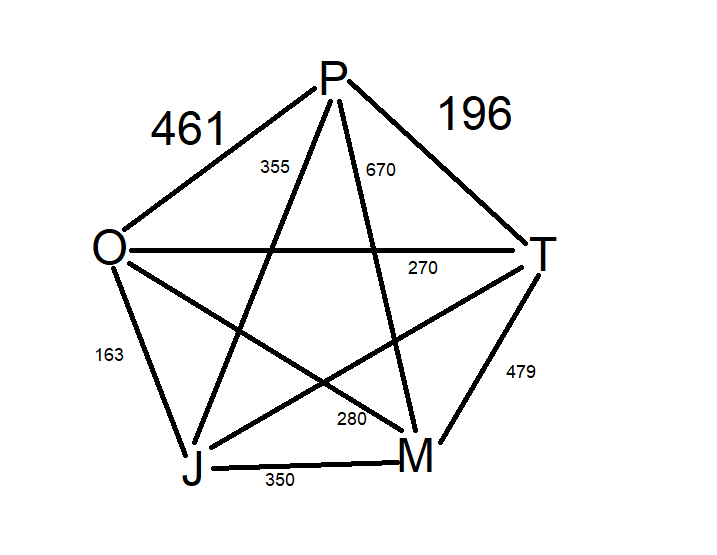
Kruskal's algorithm:
- We have to take edge with minimum distance.
- If these edge is forming cycle, then discard it. Otherwise keep it.
- Repeat step 1, until all the edges are not completed.
Applying kruskal's algorithm for above graph,
The edge with minimum distance is OJ.
Since it's not forming cycle, we will keep it.
Now, the minimum distance edge is JT. this is not forming cycle so we will keep it.
After keeping JT, the minimum distance edge from remaining edges is PT. This edge is not forming any cycle. So, we will keep it.
Now, from the remaining edges OT is minimum distance edge. But since it's forming cycle, we will discard it.
After that OM is minimum distance edge and it's not forming cycle, so we are keeping it.
After OM, JM and JP are minimum edges which forms cycle, so we will not keep them.
Now, OP and after that TM are edges with minimum distance. We will not keep them, since they are forming cycle.
Now PM is the last and minimum distance edge.
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images









