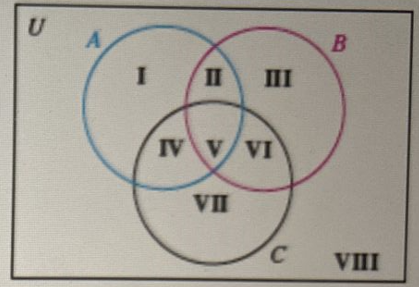
Use Venn diagrams to determine whether the following statements are equal for all sets A, B, and C. (AUB)'nc (A' UC) n (B'UC) Are the statements equal for all sets A, B, and C? O No O Yes U I II III IV V/VI VII B VIII
Use Venn diagrams to determine whether the following statements are equal for all sets A, B, and C. (AUB)'nc (A' UC) n (B'UC) Are the statements equal for all sets A, B, and C? O No O Yes U I II III IV V/VI VII B VIII
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
![**Problem Statement:**
Use Venn diagrams to determine whether the following statements are equal for all sets A, B, and C:
\[(A \cup B) \cap C\]
and
\[(A \cup C) \cap (B \cup C)\]
Are the statements equal for all sets A, B, and C?
- O No
- O Yes
**Diagram Explanation:**
The Venn diagram includes three intersecting circles labeled A, B, and C, representing the sets. The universal set U is indicated outside these circles.
The areas within the circles are labeled as follows:
- I: The part of set A that does not intersect with B or C.
- II: The intersection of sets A and B, excluding set C.
- III: The intersection of sets B and C, excluding set A.
- IV: The intersection of sets A and C, excluding set B.
- V: The intersection of all three sets, A, B, and C.
- VI: The intersection of sets A and B, excluding set C.
- VII: The intersection of sets B and C, excluding set A.
- VIII: The part of set C that does not intersect with A or B.
This problem asks whether the two expressions are equivalent by comparing their areas on a Venn diagram.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F94f92ff5-1fee-41b2-9a69-3f1799cc23e2%2F9177dcb0-e473-4ae1-a095-8dc0e2308be4%2Ftbrakh_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Use Venn diagrams to determine whether the following statements are equal for all sets A, B, and C:
\[(A \cup B) \cap C\]
and
\[(A \cup C) \cap (B \cup C)\]
Are the statements equal for all sets A, B, and C?
- O No
- O Yes
**Diagram Explanation:**
The Venn diagram includes three intersecting circles labeled A, B, and C, representing the sets. The universal set U is indicated outside these circles.
The areas within the circles are labeled as follows:
- I: The part of set A that does not intersect with B or C.
- II: The intersection of sets A and B, excluding set C.
- III: The intersection of sets B and C, excluding set A.
- IV: The intersection of sets A and C, excluding set B.
- V: The intersection of all three sets, A, B, and C.
- VI: The intersection of sets A and B, excluding set C.
- VII: The intersection of sets B and C, excluding set A.
- VIII: The part of set C that does not intersect with A or B.
This problem asks whether the two expressions are equivalent by comparing their areas on a Venn diagram.
Expert Solution
Step 1
Step by step
Solved in 2 steps with 1 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
