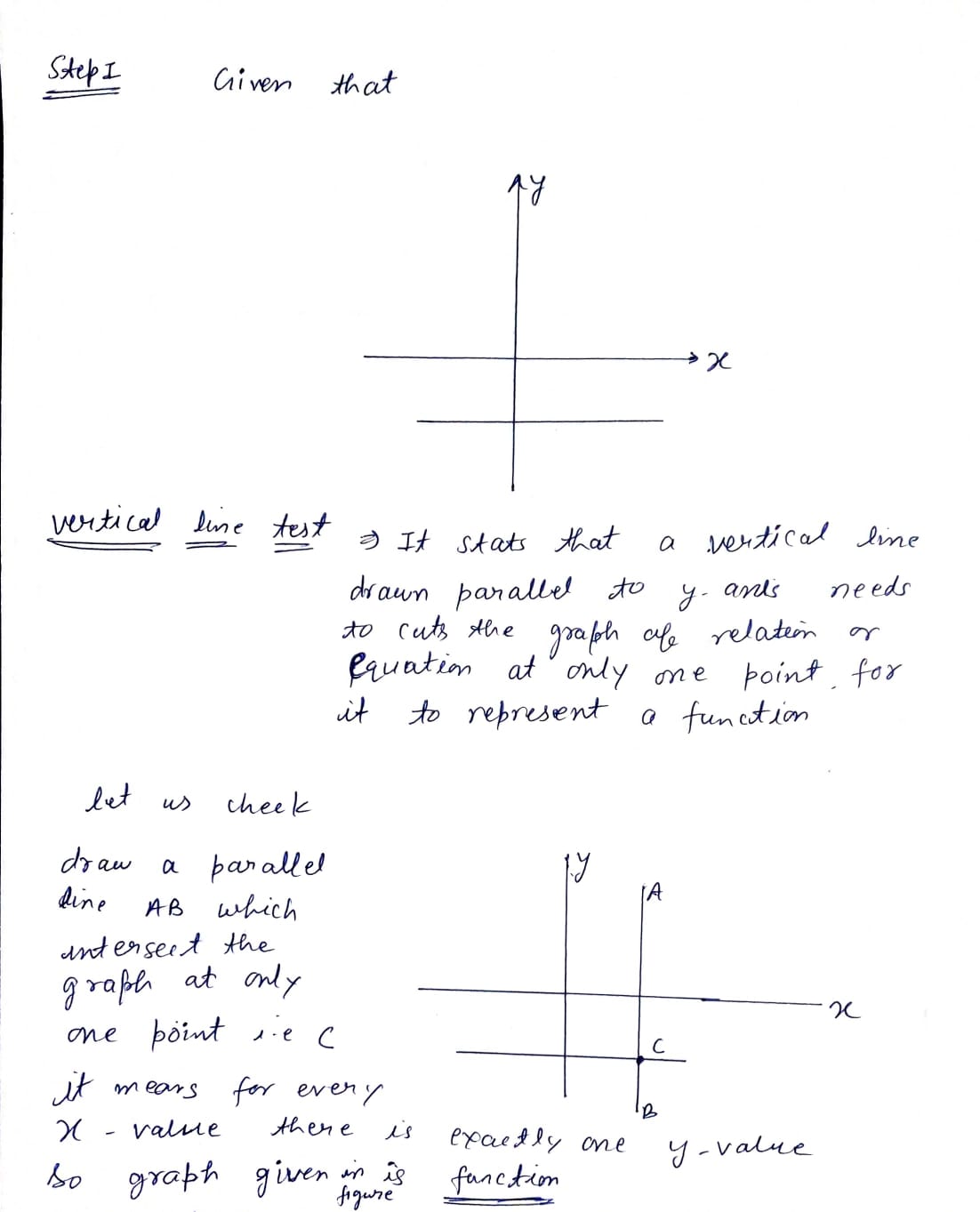
Use the vertical line test to determine whether the given graph is a graph in which y is a function of x. a graph in which y is a function of x because a vertical line The graph intersects the graph in more than one point. Thy be The be drawn such that it
Use the vertical line test to determine whether the given graph is a graph in which y is a function of x. a graph in which y is a function of x because a vertical line The graph intersects the graph in more than one point. Thy be The be drawn such that it
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Answer

Transcribed Image Text:### Vertical Line Test for Functions
**Instruction:**
Use the vertical line test to determine whether the given graph is a graph in which \( y \) is a function of \( x \).
**Diagram Explanation:**
The diagram includes a graph with axes labeled \( x \) (horizontal) and \( y \) (vertical). A vertical line is shown intersecting the graph.
**Text Explanation:**
- The graph \( \_\_\_ \) a graph in which \( y \) is a function of \( x \) because a vertical line \( \_\_\_ \) be drawn such that it intersects the graph in more than one point.
**Options:**
- The first dropdown can be filled with "is" or "is not."
- The second dropdown can be filled with "cannot" or "can."
**Important Concept:**
A vertical line can only intersect a graph at one point if \( y \) is a function of \( x \). If it intersects at more than one point, \( y \) is not a function of \( x \).
![**Title: Understanding the Vertical Line Test**
**Text:**
Use the vertical line test to determine whether the given graph is a graph in which \( y \) is a function of \( x \).
**Diagram Explanation:**
The diagram depicts a set of axes with a curve on a Cartesian plane. A vertical dotted line is drawn to intersect the curve.
**Interactive Question:**
The graph [blank] a graph in which \( y \) is a function of \( x \) because a vertical line [dropdown box] be drawn such that it intersects the graph at more than one point.
**Options:**
- is
- is not
**Note:**
The vertical line test states that a graph represents a function if and only if no vertical line intersects the graph at more than one point. This interactive section lets users apply this principle by deciding if the given graph meets this criterion.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ffebfc829-3adc-4601-a5b5-bd5b3e3c23b0%2F6c6c6dee-6fa4-4f51-a4a3-2077192ea062%2Fzc98h4b_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Title: Understanding the Vertical Line Test**
**Text:**
Use the vertical line test to determine whether the given graph is a graph in which \( y \) is a function of \( x \).
**Diagram Explanation:**
The diagram depicts a set of axes with a curve on a Cartesian plane. A vertical dotted line is drawn to intersect the curve.
**Interactive Question:**
The graph [blank] a graph in which \( y \) is a function of \( x \) because a vertical line [dropdown box] be drawn such that it intersects the graph at more than one point.
**Options:**
- is
- is not
**Note:**
The vertical line test states that a graph represents a function if and only if no vertical line intersects the graph at more than one point. This interactive section lets users apply this principle by deciding if the given graph meets this criterion.
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

