Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
![**Title: Curve Sketching of Quadratic Functions**
**Instructions:**
Use the steps to curve sketching to graph the following functions.
**Problem 3:**
\[ f(x) = x^2 - 12x + 36 \]
**Graph Explanation:**
This function is a quadratic expression, represented by a parabola. The key features you should identify and graph are:
1. **Vertex**: The vertex form of a quadratic function is helpful to identify the vertex directly. For this function, it can be transformed as such: \( f(x) = (x - 6)^2 \), indicating the vertex is at point (6, 0).
2. **Axis of Symmetry**: The axis of symmetry for this function is the vertical line \( x = 6 \).
3. **Direction**: Since the coefficient of \( x^2 \) is positive, the parabola opens upwards.
4. **Y-intercept**: When \( x = 0 \), \( f(x) = 36 \). Thus, the y-intercept is at (0, 36).
5. **X-intercepts**: The points where the graph intersects the x-axis can be found by setting \( f(x) = 0 \). Solving gives a double root at \( x = 6 \), indicating this is also the vertex.
This curve sketching approach helps in understanding the behavior of the quadratic function and plotting it accurately on a coordinate plane.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F0f9e4cd1-015a-4a96-a677-2fe562598422%2F3954c807-e53e-4d32-8f82-567381a68daf%2F36c3n0e_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Title: Curve Sketching of Quadratic Functions**
**Instructions:**
Use the steps to curve sketching to graph the following functions.
**Problem 3:**
\[ f(x) = x^2 - 12x + 36 \]
**Graph Explanation:**
This function is a quadratic expression, represented by a parabola. The key features you should identify and graph are:
1. **Vertex**: The vertex form of a quadratic function is helpful to identify the vertex directly. For this function, it can be transformed as such: \( f(x) = (x - 6)^2 \), indicating the vertex is at point (6, 0).
2. **Axis of Symmetry**: The axis of symmetry for this function is the vertical line \( x = 6 \).
3. **Direction**: Since the coefficient of \( x^2 \) is positive, the parabola opens upwards.
4. **Y-intercept**: When \( x = 0 \), \( f(x) = 36 \). Thus, the y-intercept is at (0, 36).
5. **X-intercepts**: The points where the graph intersects the x-axis can be found by setting \( f(x) = 0 \). Solving gives a double root at \( x = 6 \), indicating this is also the vertex.
This curve sketching approach helps in understanding the behavior of the quadratic function and plotting it accurately on a coordinate plane.
Expert Solution
Step 1
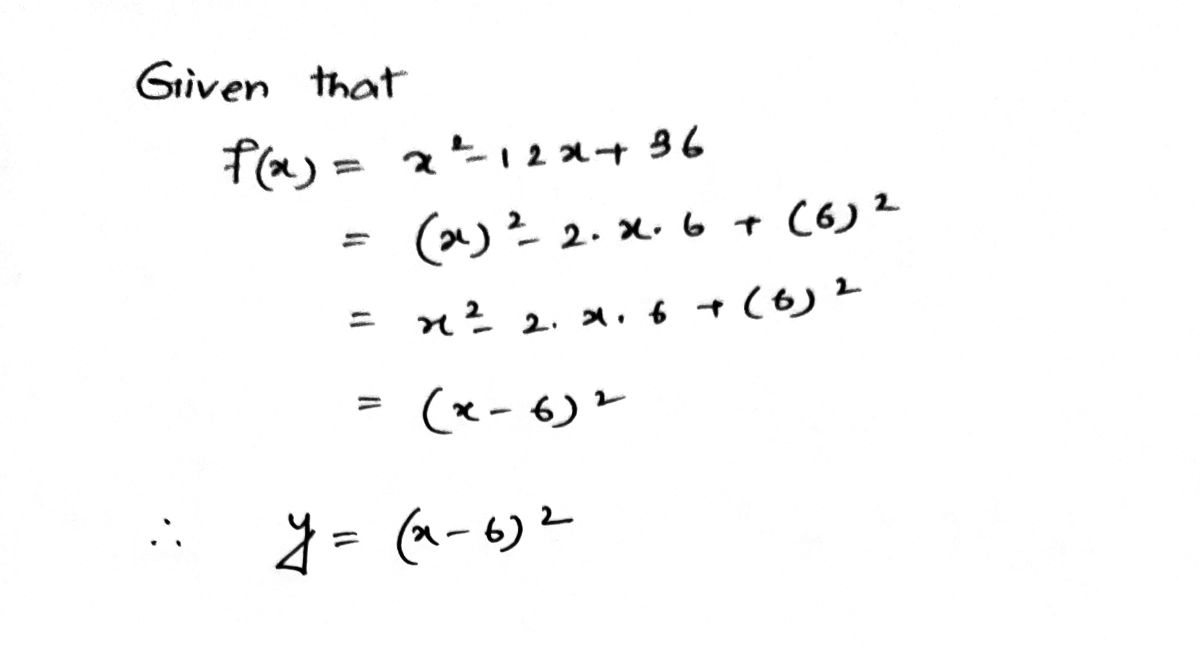
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning