## Analysis of Graphs and Calculus ProblemsThe provided graphs and questions are designed to test your understanding of derivatives and functions. Below is a detailed explanation of each element present in the graphs and questions.### Graph Details#### **Graph of $ g(x) $:**- This graph features a straight line with a positive slope.- The line passes through the x-y plane, specifically crossing the x-axis around 4.- The y-intercept of the line is approximately -8.- The slope of the line can be determined by analyzing the change in y over the change in x between any two points on the line.#### **Graph of $ h(x) $:**- This graph is characterized by two line segments forming a V-shape, indicating a piecewise linear function.- The V-shape converges at the point $ (2, 3) $, which is a sharp corner.- The line segment on the left has a negative slope while the right segment has a positive slope.- Notably, the graph has a sharp corner at $ x = 2 $, indicating a point where the derivative does not exist.### Questions and Calculations#### **12. If $ f(x) = g(x) \cdot h(x) $, find…**- **a. $ f'(0) $**- **b. $ f'(2) $**- **c. $ f'(4) $**This problem involves finding derivatives at specific points for the product of two functions. The Product Rule from calculus will be used here.#### **13. If $ f(x) = \frac{g(x)}{h(x)} $, find…**- **a. $ f'(0) $**- **b. $ f'(2) $**- **c. $ f'(4) $**This problem involves finding derivatives for the quotient of two functions, utilizing the Quotient Rule.#### **14. If $ f(x) = \frac{h(x)}{g(x)} $, find…**- **a. $ f'(0) $**- **b. $ f'(2) $**- **c. $ f'(4) $**Similar to question 13, this problem requires the use of the Quotient Rule for differentiation.### Note:For each of these questions, calculating the derivatives at the specific points

Question no. (12)If , then to find the following.Note: Since the student has posted multiple…

Answered: Use the graphs to answer the next…

Calculus: Early Transcendentals

8th Edition

ISBN:9781285741550

Author:James Stewart

Publisher:James Stewart

Chapter1: Functions And Models

Section: Chapter Questions

Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...

See similar textbooks

Related questions

Question

Expert Solution

Step 1: Define the problem.

Question no. (12)

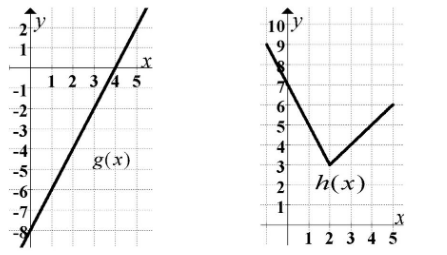
If $straight f open parentheses straight x close parentheses equals straight g open parentheses straight x close parentheses times straight h open parentheses straight x close parentheses$ , then to find the following.

$open parentheses straight a close parentheses space straight f apostrophe open parentheses 0 close parentheses open parentheses straight b close parentheses space straight f apostrophe open parentheses 2 close parentheses open parentheses straight c close parentheses space straight f apostrophe open parentheses 4 close parentheses$

Note: Since the student has posted multiple questions and does not mention
any specific question, so we are solving first question (question no. 12) according to
our guidelines. Student can re-post the remaining questions.