Use the graph to determine the function's domain and range. --2 2 20 -4- OA. Domain: [0,00) Range: (-00,00) OB. Domain: (-00,00) Range: [-2,00) OC. Domain: [0,00) Range: [-2,00) O D. Domain: [0,00) Range: [0,00)
Use the graph to determine the function's domain and range. --2 2 20 -4- OA. Domain: [0,00) Range: (-00,00) OB. Domain: (-00,00) Range: [-2,00) OC. Domain: [0,00) Range: [-2,00) O D. Domain: [0,00) Range: [0,00)
Algebra and Trigonometry (6th Edition)
6th Edition
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:Robert F. Blitzer
ChapterP: Prerequisites: Fundamental Concepts Of Algebra
Section: Chapter Questions
Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...
Related questions
Question
100%
please help with this question

Transcribed Image Text:**Transcription for Educational Website**
**Title: Determining Domain and Range from a Graph**
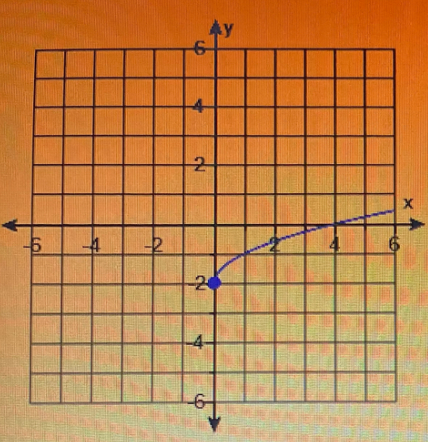
Use the graph provided to determine the function's domain and range.
**Graph Description:**
- The graph represents a function plotted on a coordinate plane.
- The x-axis and y-axis are labeled, with tick marks at intervals of 1 unit.
- The curve starts at the point (0, 2) and continues to the right, moving upwards.
- A filled circle at (0, 2) indicates that this point is included in the function.
**Multiple Choice Options:**
A. Domain: \([0, \infty)\)
Range: \((-∞, ∞)\)
B. Domain: \((-∞, ∞)\)
Range: \([2, ∞)\)
C. Domain: \([0, ∞)\)
Range: \([2, ∞)\)
D. Domain: \([0, ∞)\)
Range: \([0, ∞)\)
**Explanation:**
- **Domain**: Refers to all possible x-values for which the function is defined. From the graph, the function starts at x = 0 and extends to the right indefinitely. Thus, the domain is \([0, ∞)\).
- **Range**: Refers to all possible y-values the function can take. Starting at y = 2, the curve extends upwards indefinitely. Therefore, the range is \([2, ∞)\).
**Correct Answer: C.**
Domain: \([0, ∞)\)
Range: \([2, ∞)\)
Expert Solution
Step 1: Graph of the function
The graph of the function is
To determine: The range and domain of the function using graph.
Step by step
Solved in 3 steps with 7 images

Recommended textbooks for you

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:
9780135163078
Author:
Michael Sullivan
Publisher:
PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:
9780980232776
Author:
Gilbert Strang
Publisher:
Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:
9780077836344
Author:
Julie Miller, Donna Gerken
Publisher:
McGraw-Hill Education