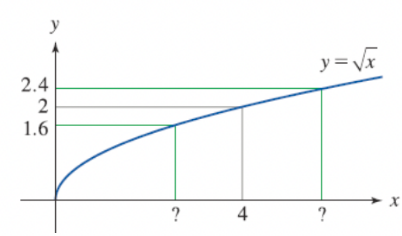
Use the given graph of f(x) = √x to find a number & such that if |x - 4| < & then √x - 2 <0.4. 8 = y 2.4 2 1.6 ? 4 y = √x ?
Use the given graph of f(x) = √x to find a number & such that if |x - 4| < & then √x - 2 <0.4. 8 = y 2.4 2 1.6 ? 4 y = √x ?
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter3: Functions And Graphs
Section3.5: Graphs Of Functions
Problem 58E
Related questions
Question
Q6. Please answer this question

Transcribed Image Text:The image presents a mathematical problem involving the function \( f(x) = \sqrt{x} \). It asks to find a number \( \delta \) such that if \( |x - 4| < \delta \), then \( |\sqrt{x} - 2| < 0.4 \).
### Graph Explanation:
- **Axes**: The graph is plotted on the Cartesian plane with the x-axis labeled as \( x \) and the y-axis labeled as \( y \).
- **Function Line**: The curve represents the function \( y = \sqrt{x} \), which steadily increases as \( x \) increases.
- **Horizontal Lines**: Two horizontal green lines are drawn at \( y = 2.4 \) and \( y = 1.6 \). These lines are used to represent the bounds within \( |\sqrt{x} - 2| < 0.4 \).
- **Vertical Lines**: Two vertical lines intersect the function curve at the points corresponding to \( y = 2.4 \) and \( y = 1.6 \). The x-coordinates of these intersections suggest the values for \( ? \) in question, and you are asked to identify these values related to \( x = 4 \).
- **Target Point**: The point on the curve where \( x = 4 \) corresponds to \( \sqrt{4} = 2 \).
### Task:
You need to define the distance \( \delta \) around \( x = 4 \) such that all \( x \) within this range (\( |x - 4| < \delta \)) have corresponding \( y \)-values on the graph within the range \( 1.6 < y < 2.4 \).
### Solution Box:
- A box labeled \(\delta =\) is provided to input the calculated \( \delta \).
Expert Solution
Step 1
Given Data:
Let us consider the given graph,
Step by step
Solved in 3 steps with 2 images

Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Holt Mcdougal Larson Pre-algebra: Student Edition…
Algebra
ISBN:
9780547587776
Author:
HOLT MCDOUGAL
Publisher:
HOLT MCDOUGAL


Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Holt Mcdougal Larson Pre-algebra: Student Edition…
Algebra
ISBN:
9780547587776
Author:
HOLT MCDOUGAL
Publisher:
HOLT MCDOUGAL


Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,