Use the fact that matrices A and B are row-equivalent. 1 2 1 25 1 1 A = 3 72 2 -2 6 13 5 -1 1 0 30-4 0 1 -1 0 B = 0 0 L0 0 0 0 0 1 -2 (a) Find the rank and nullity of A. rank nullity (b) Find a basis for the nullspace of A. (c) Find a basis for the row space of A. (d) Find a basis for the column space of A.
Use the fact that matrices A and B are row-equivalent. 1 2 1 25 1 1 A = 3 72 2 -2 6 13 5 -1 1 0 30-4 0 1 -1 0 B = 0 0 L0 0 0 0 0 1 -2 (a) Find the rank and nullity of A. rank nullity (b) Find a basis for the nullspace of A. (c) Find a basis for the row space of A. (d) Find a basis for the column space of A.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Hi I just need subpart b) and d) answered thank you!

Transcribed Image Text:Here's a transcription and explanation of the educational content from the image:
---
**Matrix and Linear Independence Analysis**
1. **(d) Find a basis for the column space of A**
- Three matrices are illustrated vertically with arrows indicating transformation or reduction. These matrices are shown in three steps, suggesting a reduction process to find a basis for the column space.
2. **(e) Determine whether or not the rows of A are linearly independent.**
- Options given:
- O independent
- O dependent
3. **(f) Let the columns of A be denoted by a₁, a₂, a₃, a₄, and a₅. Which of the following sets is (are) linearly independent? (Select all that apply)**
- Options with checkboxes:
- □ {a₁, a₂, a₃}
- □ {a₂, a₄}
- □ {a₁, a₂, a₃, a₅}
- □ {a₁, a₃, a₅}
---
The image suggests a focus on understanding linear transformations, column spaces, and linear independence in matrices, which are key concepts in linear algebra.
![The image appears to be a problem set related to linear algebra, focusing on finding the rank, nullspaces, and bases of matrices.
**Main Instructions:**
- **Use the fact that matrices A and B are row-equivalent.**
**Given Matrices:**
- \( A =
\begin{bmatrix}
2 & 5 & 7 & 1 & 0 \\
4 & 9 & 1 & 2 & 8 \\
-2 & -3 & 5 & 1 & 0
\end{bmatrix} \)
- \( B =
\begin{bmatrix}
1 & 3 & 5 & -1 & 4 \\
0 & 1 & 0 & 2 & 2 \\
0 & 0 & 1 & -1 & 0
\end{bmatrix} \)
**Tasks:**
(a) **Find the rank and nullity of A:**
- Rank: [ ]
- Nullity: [ ]
(b) **Find a basis for the nullspace of A:**
- The solution space is provided with placeholders for vectors:
\[
\begin{bmatrix}
\, \, \\
\, \, \\
\, \, \\
\, \, \\
\, \,
\end{bmatrix}
\Longrightarrow
\begin{bmatrix}
\, \, \\
\, \, \\
\, \, \\
\, \, \\
\, \,
\end{bmatrix}
\]
(c) **Find a basis for the row space of A:**
- Another placeholder for vectors:
\[
\begin{bmatrix}
\, \, \\
\, \, \\
\, \, \\
\, \, \\
\, \,
\end{bmatrix}
\Longrightarrow
\begin{bmatrix}
\, \, \\
\, \, \\
\, \,
\end{bmatrix}
\]
(d) **Find a basis for the column space of A:**
- Yet another placeholder for vectors:
\[
\begin{bmatrix}
\, \, \\
\, \, \\
\, \,](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F788d30d7-3e5d-416d-85b2-dd122fe24e5a%2Fb7a05ad4-73b9-44d3-bc68-6bf73dc271b2%2Fbsww4jt_processed.jpeg&w=3840&q=75)
Transcribed Image Text:The image appears to be a problem set related to linear algebra, focusing on finding the rank, nullspaces, and bases of matrices.
**Main Instructions:**
- **Use the fact that matrices A and B are row-equivalent.**
**Given Matrices:**
- \( A =
\begin{bmatrix}
2 & 5 & 7 & 1 & 0 \\
4 & 9 & 1 & 2 & 8 \\
-2 & -3 & 5 & 1 & 0
\end{bmatrix} \)
- \( B =
\begin{bmatrix}
1 & 3 & 5 & -1 & 4 \\
0 & 1 & 0 & 2 & 2 \\
0 & 0 & 1 & -1 & 0
\end{bmatrix} \)
**Tasks:**
(a) **Find the rank and nullity of A:**
- Rank: [ ]
- Nullity: [ ]
(b) **Find a basis for the nullspace of A:**
- The solution space is provided with placeholders for vectors:
\[
\begin{bmatrix}
\, \, \\
\, \, \\
\, \, \\
\, \, \\
\, \,
\end{bmatrix}
\Longrightarrow
\begin{bmatrix}
\, \, \\
\, \, \\
\, \, \\
\, \, \\
\, \,
\end{bmatrix}
\]
(c) **Find a basis for the row space of A:**
- Another placeholder for vectors:
\[
\begin{bmatrix}
\, \, \\
\, \, \\
\, \, \\
\, \, \\
\, \,
\end{bmatrix}
\Longrightarrow
\begin{bmatrix}
\, \, \\
\, \, \\
\, \,
\end{bmatrix}
\]
(d) **Find a basis for the column space of A:**
- Yet another placeholder for vectors:
\[
\begin{bmatrix}
\, \, \\
\, \, \\
\, \,
Expert Solution
Step 1
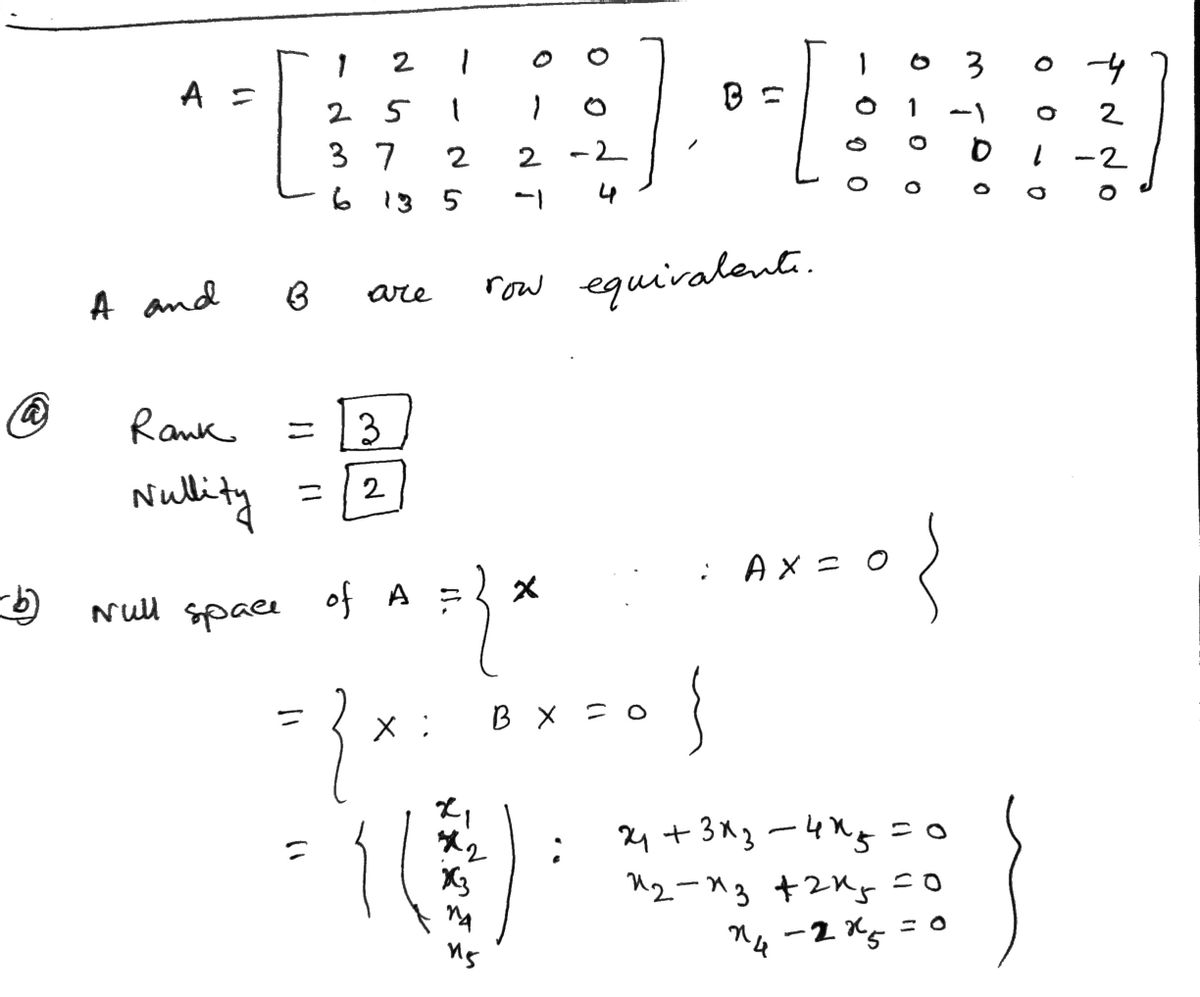
Step by step
Solved in 5 steps with 5 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

