Use the definition of convergence to prove lim 1 11 7²27-1 = 0; no theorem in
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
can you use the same proof like example to do this question?

Transcribed Image Text:4. Use the definition of convergence to prove lim¹ = 0; no theorem in
Ross 9 is allowed.

Transcribed Image Text:Formal Proof
Let e > 0 and let N max{2, ₁√√54}. Then n > N implies n >
hence 54 < €,
also 27n3n+24.
and hence
as desired.
27n
hence
lim
=
[4n³ + 3n
n³ - 6
3n+ 24
n³
6
23
n³/2 < €. Since n > 2, we have n ≤n³ - 6 and
Thus n > N implies
2
<
=
= lim
4n³ + 3n
n³-6
27n
}n3
4
Example 3 illustrates direct proofs of even rather simple limits
can get complicated. With the limit theorems of §9 we would just
write
54
n²
< €₂
4|<₁₂
4 < €,
=
54
lim 4+3 · lim(2)
lim 1-6-lim(3)
€ 9
= 4.
Expert Solution
Step 1: Definition of convergence of a real sequence
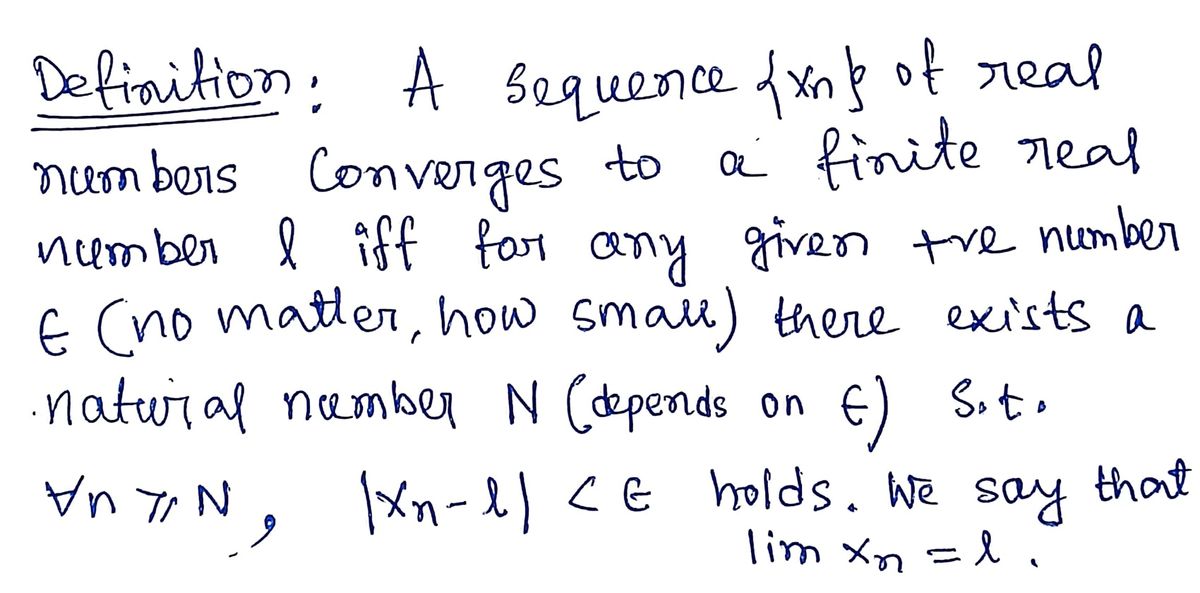
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

