Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question

Transcribed Image Text:**Synthetic Division Problem**
**Task:**
Use synthetic division to divide the polynomial \(x^3 + 4x^2 - 14x - 14\) by \(x - 3\).
**Setup:**
- The divisor is \(x - 3\), so the root used in synthetic division is \(3\).
- The coefficients of the polynomial are \(1, 4, -14, -14\).
**Process:**
1. Write the coefficients in a row:
\(1, 4, -14, -14\)
2. Draw a horizontal and vertical line to separate the setup.
3. Place the number \(3\) (from \(x - 3\)) to the left of the vertical line.
4. Below the first coefficient (1), draw a line and copy it down. This is your starting point.
5. Multiply the first coefficient by \(3\) and write the result under the next coefficient.
6. Add this result to the next coefficient. Write the sum below.
7. Repeat the multiplication, moving the results across the coefficients.
8. The last result is the remainder.
**Fields to fill in:**
- Boxes are provided for the calculation steps.
- Fields for the final quotient and remainder are available.
**Results:**
- **The quotient is:** (Fill in after calculating)
- **The remainder is:** (Fill in after calculating)
**Action:**
- Click the “Check Answer” button to verify your solution.
Expert Solution
Step 1
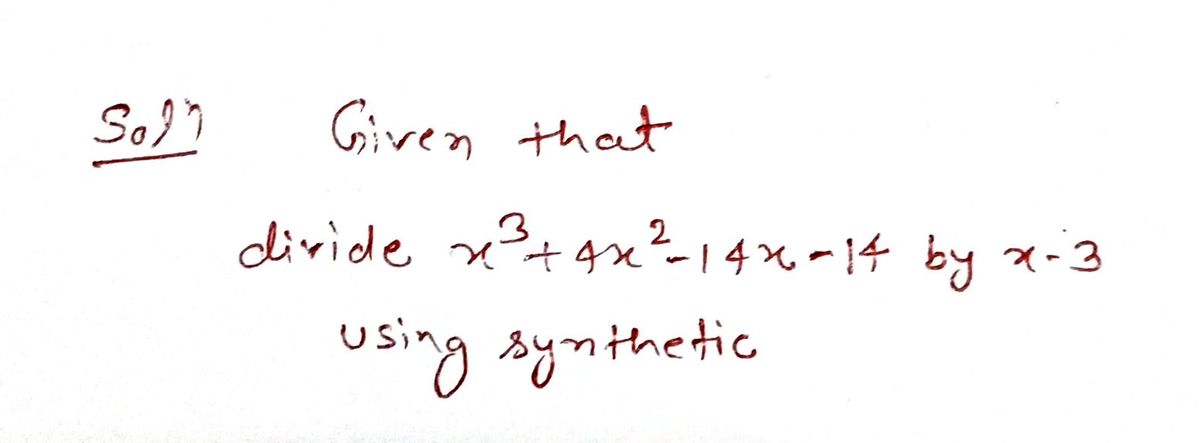
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning