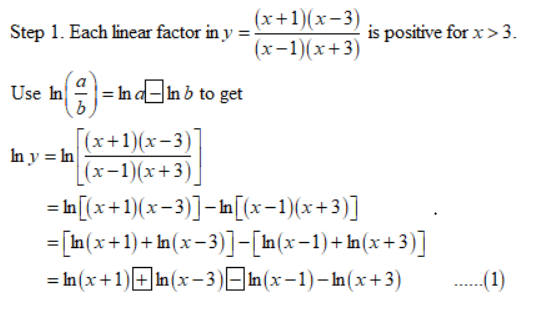Use logarithmic differentiation to find dy/dx. y = (x + 1)(x-3) x>3 Step 1 The given function y is positive for all x greater than three. Hence, the function In y is defined defined in the domain of x. Obtain the natural logarithm of the function y, using the logarithmic properties In ab = In a + In band In()- In a ✔ In b, where a and b are positive. In y = In(x + 1) + Step 2 Use the rule for logarithmic differentiation, (in x) = Obtain the derivative, 1 Step 3 Simplify the expression. dy dx x+ = -(x1+x²3-x-1-x+3) Rearrange the terms on the right side. dy- = y dy -(1-x²1+x²3-x+3) - +In(x-3)-In(x-1)-In(x+3) Step 4 Consider the first two terms on the right side and simplify them, then consider the last two terms and simplify them separately. x+3-x+33 x-1-x-11 (x+1)(x-1) (x-33 x(x+3) 1 dy (x+1)(x-3) (x - 1)(x+3) L(x + 1)(x - 1)³ + 1 x-3 (x-1)²(x+3) ² (x-1) (x+3) (x-1)- (x+3) Step 5 Substitute the expression for y=(x + 1)(x+3) on the right side of the equation and simplify. +y +y -(x-3)(x + 3)- 1 x Your answer cannot be understood or graded. More Information (x-3)(x + 3) + [ (x + 3 X(x-1)(x-1 [2(+² -1 -√(x²+3) x²+12) ]) + 6(x_{ Your answer cannot be understood or graded. More Information (x + 1)(x-1) )(x + 3)
Use logarithmic differentiation to find dy/dx. y = (x + 1)(x-3) x>3 Step 1 The given function y is positive for all x greater than three. Hence, the function In y is defined defined in the domain of x. Obtain the natural logarithm of the function y, using the logarithmic properties In ab = In a + In band In()- In a ✔ In b, where a and b are positive. In y = In(x + 1) + Step 2 Use the rule for logarithmic differentiation, (in x) = Obtain the derivative, 1 Step 3 Simplify the expression. dy dx x+ = -(x1+x²3-x-1-x+3) Rearrange the terms on the right side. dy- = y dy -(1-x²1+x²3-x+3) - +In(x-3)-In(x-1)-In(x+3) Step 4 Consider the first two terms on the right side and simplify them, then consider the last two terms and simplify them separately. x+3-x+33 x-1-x-11 (x+1)(x-1) (x-33 x(x+3) 1 dy (x+1)(x-3) (x - 1)(x+3) L(x + 1)(x - 1)³ + 1 x-3 (x-1)²(x+3) ² (x-1) (x+3) (x-1)- (x+3) Step 5 Substitute the expression for y=(x + 1)(x+3) on the right side of the equation and simplify. +y +y -(x-3)(x + 3)- 1 x Your answer cannot be understood or graded. More Information (x-3)(x + 3) + [ (x + 3 X(x-1)(x-1 [2(+² -1 -√(x²+3) x²+12) ]) + 6(x_{ Your answer cannot be understood or graded. More Information (x + 1)(x-1) )(x + 3)
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
![Use logarithmic differentiation to find dy/dx.
y = (x + 1)(x=3), x>3
- +
Step 1
The given function y is positive for all x greater than three. Hence, the function In y is defined → defined in the domain of x. Obtain the natural logarithm of the function y, using the logarithmic properties In ab = In a + In b and In
are positive.
In(2/2) =
In y = In(x + 1)
Step 2
Use the rule for logarithmic differentiation,
d (In x)
dx
Obtain the derivative,
1
Step 3
Simplify the expression.
dy
dx
Step 5
dy
dx
dy
dx
dy = y
dx
dy
dx
=
Rearrange the terms on the right side.
= y
dy
y dx x +
(x - 1)
(x - 1)
(x - 1)
1
y
2
=
X
(x + 1)(x − 3)
(x - 1)(x + 3)
(x +
1
x + 1
x-1-x-
1
1
1
1
y
( x + 1 + x ² 3 − x ² ₁ - x + 3)
-
- 1
Substitute the expression for y =
+ In(x − 3)
Step 4
Consider the first two terms on the right side and simplify them, then consider the last two terms and simplify them separately.
1
-2
(x + 1)(x - 1)
1
(x + 3)
1
(x + 3)
(x + 3)
2
1
x - 1
+
1 )(x - 1)
+
+ y
1
x - 3
1
x - 3
+y
2
In(x - 1) - In(x + 3)
1
x - 1
(x
1
x + 3.
(x − 3)(x + 3).
-
x + 3x +
x +
1
] x² + 12)
(x² + 3)
3
3)(x + 3)
(x + 1)(x − 3) on the right side of the equation and simplify.
1)(x + 3)
(x
-
* Your answer cannot be understood or graded. More Information (x − 3)(x + 3) +
(x + 3
|)(x - 1)(x - 1
Your answer cannot be understood or graded. More Information (x + 1)(x − 1)
)(x + 3)
= In a
In b, where a and b](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ff9b6a03f-2298-4441-ab19-fb50f28ec42f%2F3b8e1dfa-0e51-4d34-b3e7-526c31c489e0%2Fmi8czmj_processed.png&w=3840&q=75)
Transcribed Image Text:Use logarithmic differentiation to find dy/dx.
y = (x + 1)(x=3), x>3
- +
Step 1
The given function y is positive for all x greater than three. Hence, the function In y is defined → defined in the domain of x. Obtain the natural logarithm of the function y, using the logarithmic properties In ab = In a + In b and In
are positive.
In(2/2) =
In y = In(x + 1)
Step 2
Use the rule for logarithmic differentiation,
d (In x)
dx
Obtain the derivative,
1
Step 3
Simplify the expression.
dy
dx
Step 5
dy
dx
dy
dx
dy = y
dx
dy
dx
=
Rearrange the terms on the right side.
= y
dy
y dx x +
(x - 1)
(x - 1)
(x - 1)
1
y
2
=
X
(x + 1)(x − 3)
(x - 1)(x + 3)
(x +
1
x + 1
x-1-x-
1
1
1
1
y
( x + 1 + x ² 3 − x ² ₁ - x + 3)
-
- 1
Substitute the expression for y =
+ In(x − 3)
Step 4
Consider the first two terms on the right side and simplify them, then consider the last two terms and simplify them separately.
1
-2
(x + 1)(x - 1)
1
(x + 3)
1
(x + 3)
(x + 3)
2
1
x - 1
+
1 )(x - 1)
+
+ y
1
x - 3
1
x - 3
+y
2
In(x - 1) - In(x + 3)
1
x - 1
(x
1
x + 3.
(x − 3)(x + 3).
-
x + 3x +
x +
1
] x² + 12)
(x² + 3)
3
3)(x + 3)
(x + 1)(x − 3) on the right side of the equation and simplify.
1)(x + 3)
(x
-
* Your answer cannot be understood or graded. More Information (x − 3)(x + 3) +
(x + 3
|)(x - 1)(x - 1
Your answer cannot be understood or graded. More Information (x + 1)(x − 1)
)(x + 3)
= In a
In b, where a and b
Expert Solution
Step 1: Fill the empty boxes in step1
Step by step
Solved in 6 steps with 6 images
Recommended textbooks for you
Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning