Use Lagrange multipliers to find the global min and max of the provided function on the provided region R: f(x,y) = x - y - xy on the triangle R with vertices (0,0), (0,2), and (4,0).
Use Lagrange multipliers to find the global min and max of the provided function on the provided region R: f(x,y) = x - y - xy on the triangle R with vertices (0,0), (0,2), and (4,0).
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Use Lagrange multipliers to find the global min and max of the provided function on the provided region R:
f(x,y) = x - y - xy on the triangle R with vertices (0,0), (0,2), and (4,0).
(See attatched image for hint)
![### Method of Lagrange Multipliers
To find the maximum and minimum values of \( f(x, y, z) \) subject to the constraint \( g(x, y, z) = k \) [assuming that these extreme values exist and \( \nabla g \neq 0 \) on the surface \( g(x, y, z) = k \)]:
(a) **Find all values of \( x, y, z, \) and \( \lambda \) such that**
\[
\nabla f(x, y, z) = \lambda \nabla g(x, y, z)
\]
and
\[
g(x, y, z) = k
\]
(b) **Evaluate \( f \) at all the points \( (x, y, z) \) that result from step (a).** The largest of these values is the maximum value of \( f \); the smallest is the minimum value of \( f \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fa09b7e9e-7b17-49fc-9ca3-114d31af39de%2Fbdb901e4-1be7-4586-91d9-c24ef17132a8%2Fp0tpxk_processed.png&w=3840&q=75)
Transcribed Image Text:### Method of Lagrange Multipliers
To find the maximum and minimum values of \( f(x, y, z) \) subject to the constraint \( g(x, y, z) = k \) [assuming that these extreme values exist and \( \nabla g \neq 0 \) on the surface \( g(x, y, z) = k \)]:
(a) **Find all values of \( x, y, z, \) and \( \lambda \) such that**
\[
\nabla f(x, y, z) = \lambda \nabla g(x, y, z)
\]
and
\[
g(x, y, z) = k
\]
(b) **Evaluate \( f \) at all the points \( (x, y, z) \) that result from step (a).** The largest of these values is the maximum value of \( f \); the smallest is the minimum value of \( f \).
Expert Solution
Step 1
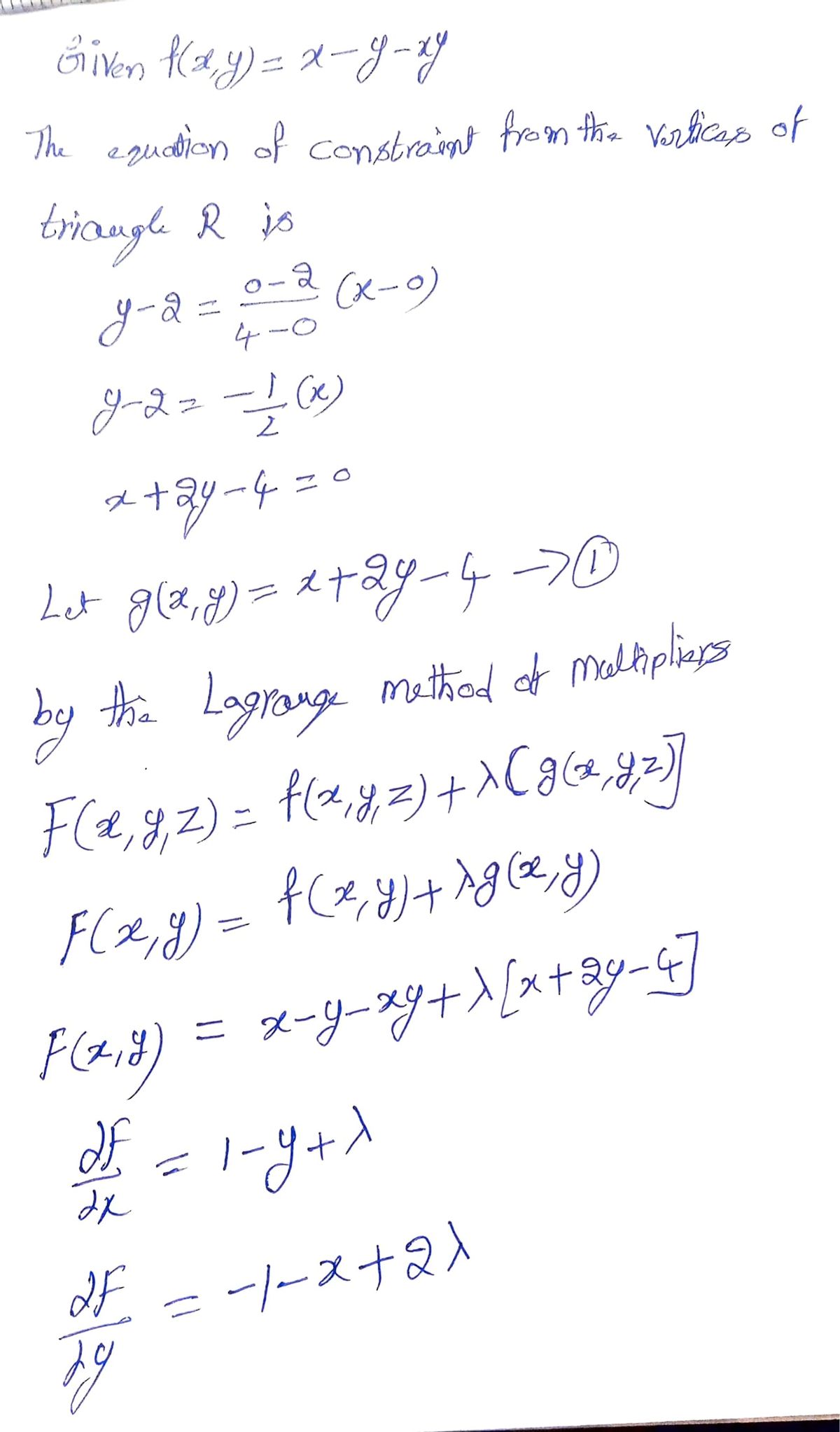
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

