Answered: Use Gauss's Law in to solve problems 1… | bartleby

Related questions

Question

Use Gauss's Law in to solve problems 1 to 3, showing and justifying your
steps and using related conceptual diagrams and mathematical formula as
needed.
(1) Find the Electric Field outside an infinitely long slab with
uniform charge density sigma.
(2): Find the Electric Field (a) outside and (b) inside a non-conducting solid
sphere with uniformly distributed charge Q.
(3) Find the Electric Field outside an infinitely long rod with uniform charge
density lambda.

Expert Solution

Step 1

Solution:

Gauss law state that the electric flux through any closed surface is equal to $\frac{1}{ε_{0}}$ times the net charge enclosed within the surface.

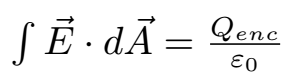
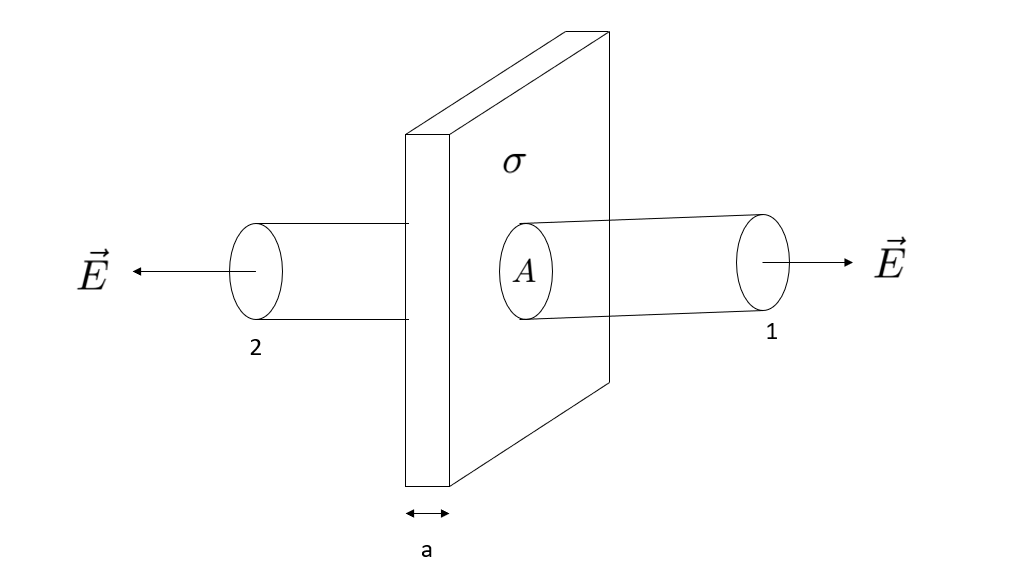
1) Let us consider the infinitely long slab of thickness 'a' having a surface charge density $σ$ . Let us construct the Gaussian surface in the form of a cylinder across the slab.

Step by step

Solved in 6 steps with 10 images

SEE SOLUTION Check out a sample Q&A here

Blurred answer

Similar questions

Please asap
Problem situation: "A sphere of radius R has a total charge Q. The volume charge density (C/m^3) within the sphere is p(r) = C/r^2, where C is a constant to be determined."part A: I solved this successfully.part B: This is where I'm stuck: "Use Gauss's Law to find the Electric Field Strength E inside the sphere, r I tried (Q*r)/(4*pi*e0*R^3) and (p*r)/(3*e0) but Pearson won't accept either answer.
(a) A rod of length 2L with uniform charge density λ is oriented along the z-axis, centered at z = 0. Find the electric field at any point on the xy plane a distance r from the rod. (Note that the figure corresponds to part c only). (b) Use your result from the previous part to show that the electric field a distance r from an infinite rod is 2λ 4πǫ0r . (c) Suppose a section with length 2L is cut out of the infinite rod. Let the center of the cut out section correspond to z = 0 as shown. Find the E-field a distance r from the z-axis in the x-y plane.
Consider two long, thin, concentric cylindrical shells. The smaller shell has a radius ‘a’ and carries a uniform surface charge density +σ. The larger shell has a radius ‘b’ and carries a surface charge density −2σ. Your answers for this problem should only depend on the variables r, σ, and ε0. A section of the two cylinders is shown to the right. (a) Find an expression for the electric field as a function of r (distance from the center of the cylinders), for r < a. (b) Find an expression for the electric field as a function of r, for a < r < b. (c) Find an expression for the electric field as a function of r, for r > b.
Both of them, please.
A charge of uniform linear density A is distributed along a long, thin, nonconducting rod. The rod is coaxial with a long conducting cylindrical shell (inner radius r, outer radius R). The net charge on the shell is zero. NOTE: Express your answers in terms of the given variables using €0 when necessary. (a) What is the magnitude of the electric field a distance d from the axis of the shell (where d > R)? Ed (b) What is the surface charge density on the inner surface of the shell? (c) What is the surface charge density on the outer surface of the shell?
Please asap
Problem Using the method of integration, what is the electric field of a uniformly charged thin circular plate (with radius R and total charge Q) at xo distance from its center? (Consider that the surface of the plate lies in the yz plane) Solution A perfect approach to this is to first obtain the E-field produced by an infinitesimal charge component of the charge Q. There will be several approaches to do this, but the most familiar to us is to obtain a very small shape that could easily represent our circular plane. That shape would be a ring. So for a ring whose charge is q, we recall that the electric field it produces at distance x0 is given by E = (1/ )(xOq)/( 2472) Since, the actual ring (whose charge is dq) we will be dealing with is an infinitesimal part of the circular plane, then, its infinitesimal electric field contribution is expressed as = (1/ )(x0 24 We wish to obtain the complete electric field contribution from the above equation, so we integrate it from 0 to R to…
A 2D annulus (thick ring) has an inner radius Ri and outer radius Ro, and charge Q non-uniformlydistributed over its surface. The 2D charge density varies with radius r by η(r)=Cr 4 for Ri ≤ r ≤ Roand η=0 for all other r. C is a constant. Answer the following in terms of the variables given above. Note: Gauss' Law will not be useful here.a) Find an expression for C such that the total charge of the annulus is Q. Include the SI units for C next to your answer.Do the units make sense?b) Draw a clear picture and use it to set up the integral to calculate the E-field at a point on the axis of the annulus (this axis is perpendicular to the plane of the annulus) a distance z from the center of the annulus. *** You must complete all the steps short of computing the integral (i.e. your eventual answer must be an integral with only ONE variable of integration and all other variables constant.) Show that your answer has the correct SI units for the electric field.
For this question, Figure 2 (see image). Consider the electric field of a disk of radius R and surface charge density σ along the z-axis as: (see image) a) Use this expression to find the electric field of the disk very close to the disk i.e. Z << R such that the disk looks like an infinite plane with surface charge density σ. b) Use a Gaussian cylinder (pill box) to find the electric field of the plate at this limit (Z << R such that the disk looks like an infinite plane), and compare it with your answer from part a.
You have a very (infinitely) long solid conducting cylinder with length L, base radius R, and total charge +Q. (a) Use Gauss’s law to find the electric field vector inside and outside the cylinder. Explain your reasoning. You can give a verbal description of the electric field vector direction. (b) Similar to how we found the electric field outside a conducting sphere to look like that of a point particle, what does the electric field outside the cylinder look like? (c) Would the electric field inside the cylinder stay the same if the cylinder was instead insulating and uniformly charged? Explain why or why not?
Can someone please help with the following questions? I've attached the pictures below. I appreciate it! For the problem that asks about the meaning of of p0, I already have the answer for that, I just need help with part b.

SEE MORE QUESTIONS