Use Euler's method to obtain a four-decimal approximation of the indicated value. Carry out the recursion of (3) in Section 2.6 Yn + 1 = Yn + hf(Xn, Yn) (3) by hand, first using h = 0.1 and then using h = 0.05. y' = 2x - 3y + 1, y(1) = 2; y(1.2) y(1.2) y(1.2) (h = 0.1) (h = 0.05)
Use Euler's method to obtain a four-decimal approximation of the indicated value. Carry out the recursion of (3) in Section 2.6 Yn + 1 = Yn + hf(Xn, Yn) (3) by hand, first using h = 0.1 and then using h = 0.05. y' = 2x - 3y + 1, y(1) = 2; y(1.2) y(1.2) y(1.2) (h = 0.1) (h = 0.05)
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Discrete Math
![**Euler's Method for Approximating Solutions to Differential Equations**
To approximate the solution of a differential equation using Euler's Method, follow these steps:
1. **Equation and Initial Conditions:**
- Differential Equation: \( y' = 2x - 3y + 1 \)
- Initial Condition: \( y(1) = 2 \)
2. **Objective:**
- Estimate \( y(1.2) \) with two different step sizes:
- \( h = 0.1 \)
- \( h = 0.05 \)
3. **Euler's Formula:**
\[
y_{n+1} = y_n + h \cdot f(x_n, y_n)
\]
Here, \( f(x, y) = 2x - 3y + 1 \).
4. **Procedure:**
- Start with the initial condition \( (x_0, y_0) \) = (1, 2).
- Use the step size \( h \) to increment \( x \).
- Calculate successive \( y \) values using Euler's formula.
5. **Calculations:**
- **For \( h = 0.1 \):**
- Calculate \( y \) at \( x = 1.1 \).
- Then calculate \( y \) at \( x = 1.2 \).
- **For \( h = 0.05 \):**
- Calculate \( y \) at \( x = 1.05 \).
- Continue to \( x = 1.1 \), then \( 1.15 \), and finally \( 1.2 \).
6. **Boxes for Solutions:**
- \( y(1.2) \approx \) \[\boxed{}\] *(when \( h=0.1 \))*
- \( y(1.2) \approx \) \[\boxed{}\] *(when \( h=0.05 \))*
**Note:** The detailed calculations can be filled in the boxes using the above method step-by-step.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fc42b80bf-a5d4-414b-bce1-0fe52a04dbbd%2F5edf5b39-d6a5-4aa8-ba3d-a32a249990f6%2Fdxvyn1s_processed.png&w=3840&q=75)
Transcribed Image Text:**Euler's Method for Approximating Solutions to Differential Equations**
To approximate the solution of a differential equation using Euler's Method, follow these steps:
1. **Equation and Initial Conditions:**
- Differential Equation: \( y' = 2x - 3y + 1 \)
- Initial Condition: \( y(1) = 2 \)
2. **Objective:**
- Estimate \( y(1.2) \) with two different step sizes:
- \( h = 0.1 \)
- \( h = 0.05 \)
3. **Euler's Formula:**
\[
y_{n+1} = y_n + h \cdot f(x_n, y_n)
\]
Here, \( f(x, y) = 2x - 3y + 1 \).
4. **Procedure:**
- Start with the initial condition \( (x_0, y_0) \) = (1, 2).
- Use the step size \( h \) to increment \( x \).
- Calculate successive \( y \) values using Euler's formula.
5. **Calculations:**
- **For \( h = 0.1 \):**
- Calculate \( y \) at \( x = 1.1 \).
- Then calculate \( y \) at \( x = 1.2 \).
- **For \( h = 0.05 \):**
- Calculate \( y \) at \( x = 1.05 \).
- Continue to \( x = 1.1 \), then \( 1.15 \), and finally \( 1.2 \).
6. **Boxes for Solutions:**
- \( y(1.2) \approx \) \[\boxed{}\] *(when \( h=0.1 \))*
- \( y(1.2) \approx \) \[\boxed{}\] *(when \( h=0.05 \))*
**Note:** The detailed calculations can be filled in the boxes using the above method step-by-step.
Expert Solution
Step 1
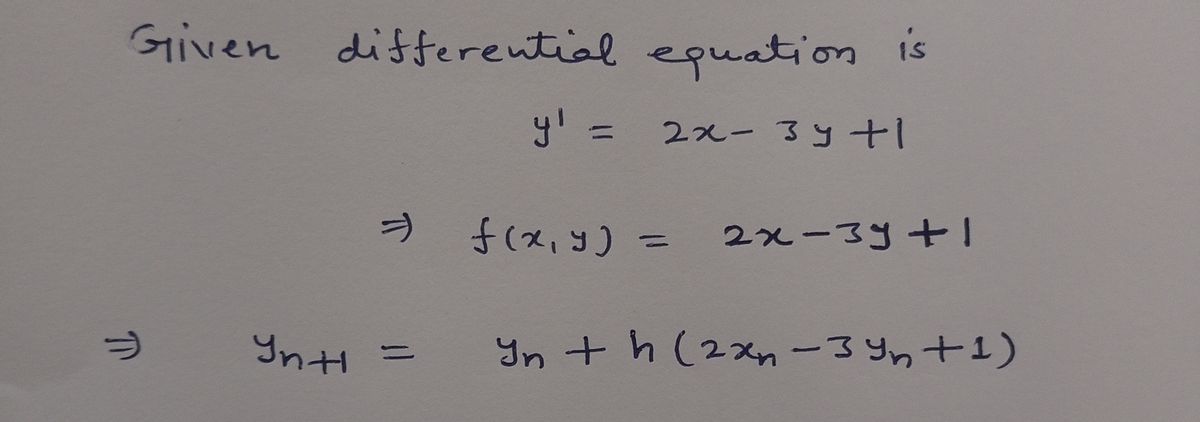
Step by step
Solved in 4 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

