Use calculus to find the function f(t) that solves the following conditions: df = k - f(t) and f(0) = 1, where k € R is a constant. Using what you know about the derivatives of sine and cosine, find the derivative of cis(kt) with respect to t. (Note that i is a constant, and behaves just like a real constant with respect to differentiation.) By comparing your previous two results, explain why cis (kt) is frequently written as ekt
Use calculus to find the function f(t) that solves the following conditions: df = k - f(t) and f(0) = 1, where k € R is a constant. Using what you know about the derivatives of sine and cosine, find the derivative of cis(kt) with respect to t. (Note that i is a constant, and behaves just like a real constant with respect to differentiation.) By comparing your previous two results, explain why cis (kt) is frequently written as ekt
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Please do Exercise 1 part A.B,C and please show step by step and explain.

Transcribed Image Text:Introduction
This problem is designed to give you some idea how complex numbers are used in communications engi-
neering. Indeed, complex numbers are the foundation of the part of communications engineering known
as digital signal processing.
Complex waves
You may or may not know that communications signals are sent as waves: cosines and sines. We will
show there is a deep relation between complex exponential functions and cosines and sines. We will take
advantage of this to develop formulas for analyzing signals that are actually used in practice.
Exercise 1.
(a) Use calculus to find the function f(t) that solves the following conditions: df = k. f(t) and f(0) = 1,
where k € R is a constant.
(b) Using what you know about the derivatives of sine and cosine, find the derivative of cis(kt) with respect
to t. (Note that i is a constant, and behaves just like a real constant with respect to differentiation.)
(c) By comparing your previous two results, explain why cis (kt) is frequently written as eikt
From now on, I'll be using the notation eie instead of cis(0). This is the notation that is used in all advanced
mathematics, physics, and engineering references.
Expert Solution
Step 1
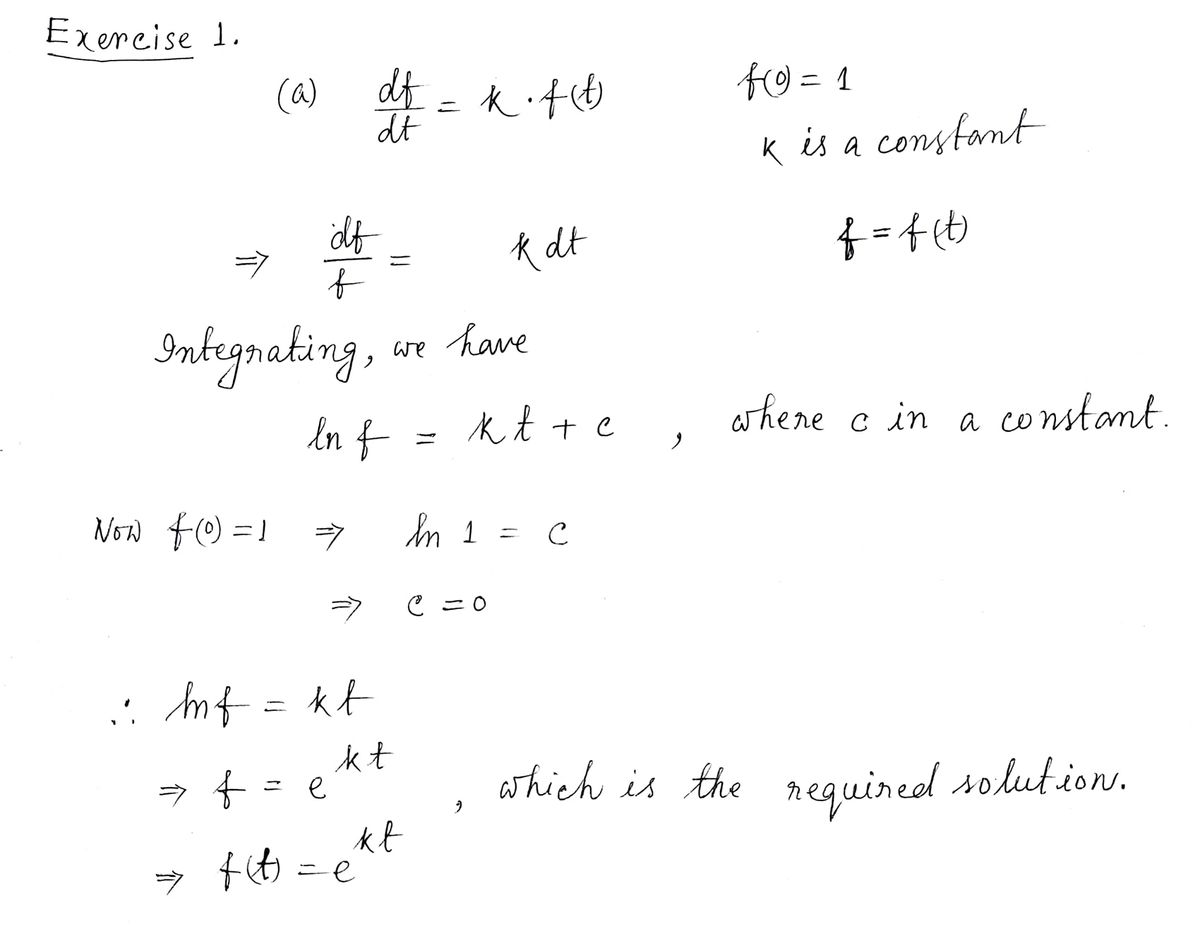
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

