Two dice are rolled. Find the probabilities of the following, as reduced fractions, and justify. Use the formula sheet if needed for help. a. Both dice are ≥4, given that the sum is ≥9.
Two dice are rolled. Find the probabilities of the following, as reduced fractions, and justify. Use the formula sheet if needed for help. a. Both dice are ≥4, given that the sum is ≥9.
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
2. Two dice are rolled. Find the probabilities of the following, as reduced fractions, and justify. Use the formula sheet if needed for help.
a. Both dice are ≥4, given that the sum is ≥9.
![**Basic Probability Principle**
\[ P(E) = \frac{n(E)}{n(S)} \]
**Conditional Probability**
\[ P(E|F) = \frac{n(E \cap F)}{n(F)} = \frac{P(E \cap F)}{P(F)} \]
**Union Rule**
- For sets: \( n(A \cup B) = n(A) + n(B) - n(A \cap B) \)
- For probability: \( P(E \cup F) = P(E) + P(F) - P(E \cap F) \)
**Number of Subsets**
- If a set has \( n \) elements, then it has \( 2^n \) subsets.
**Product Rule**
\[ P(E \cap F) = P(E) \cdot P(F|E) = P(F) \cdot P(E|F) \]
**Odds**
\[ \text{Odds in favor of } E = \frac{P(E)}{P(E')} \]
If odds in favor of \( E \) are \( m : n \), then
\[ P(E) = \frac{m}{m+n} \]
**Complement Rule (Probability)**
\[ P(E') = 1 - P(E) \]
\[ P(E) = 1 - P(E') \]
**Complement Rule (Number of Outcomes)**
\[ n(E) = n(S) - n(E') \]
\[ n(E') = n(S) - n(E) \]
**Bayes' Theorem**
\[ P(F|E) = \frac{P(E|F)P(F)}{P(E)} \]
Special Case:
\[ P(F|E) = \frac{P(F)P(E|F)}{P(E|F)P(F) + P(E|F')P(F')} \]
**Independent Events**
\[ P(E|F) = P(E) \]
\[ P(F|E) = P(F) \]
\[ P(E \cap F) = P(E) \cdot P(F) \]
**Permutations**
\[ P(n, k) = \frac{n!}{(n-k)!} \]
**Combinations**
\[ C(n, k) = \frac{n!}{k!(n-k)!} \]
**Distinguishable Permutations**
\[ \frac{n!}{n](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F985fbbf0-f8fa-4c87-a1a5-f926559935c9%2F381f71a0-a06b-4127-9795-d25731eafbf2%2Ff7sl9i_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Basic Probability Principle**
\[ P(E) = \frac{n(E)}{n(S)} \]
**Conditional Probability**
\[ P(E|F) = \frac{n(E \cap F)}{n(F)} = \frac{P(E \cap F)}{P(F)} \]
**Union Rule**
- For sets: \( n(A \cup B) = n(A) + n(B) - n(A \cap B) \)
- For probability: \( P(E \cup F) = P(E) + P(F) - P(E \cap F) \)
**Number of Subsets**
- If a set has \( n \) elements, then it has \( 2^n \) subsets.
**Product Rule**
\[ P(E \cap F) = P(E) \cdot P(F|E) = P(F) \cdot P(E|F) \]
**Odds**
\[ \text{Odds in favor of } E = \frac{P(E)}{P(E')} \]
If odds in favor of \( E \) are \( m : n \), then
\[ P(E) = \frac{m}{m+n} \]
**Complement Rule (Probability)**
\[ P(E') = 1 - P(E) \]
\[ P(E) = 1 - P(E') \]
**Complement Rule (Number of Outcomes)**
\[ n(E) = n(S) - n(E') \]
\[ n(E') = n(S) - n(E) \]
**Bayes' Theorem**
\[ P(F|E) = \frac{P(E|F)P(F)}{P(E)} \]
Special Case:
\[ P(F|E) = \frac{P(F)P(E|F)}{P(E|F)P(F) + P(E|F')P(F')} \]
**Independent Events**
\[ P(E|F) = P(E) \]
\[ P(F|E) = P(F) \]
\[ P(E \cap F) = P(E) \cdot P(F) \]
**Permutations**
\[ P(n, k) = \frac{n!}{(n-k)!} \]
**Combinations**
\[ C(n, k) = \frac{n!}{k!(n-k)!} \]
**Distinguishable Permutations**
\[ \frac{n!}{n
Expert Solution
Step 1
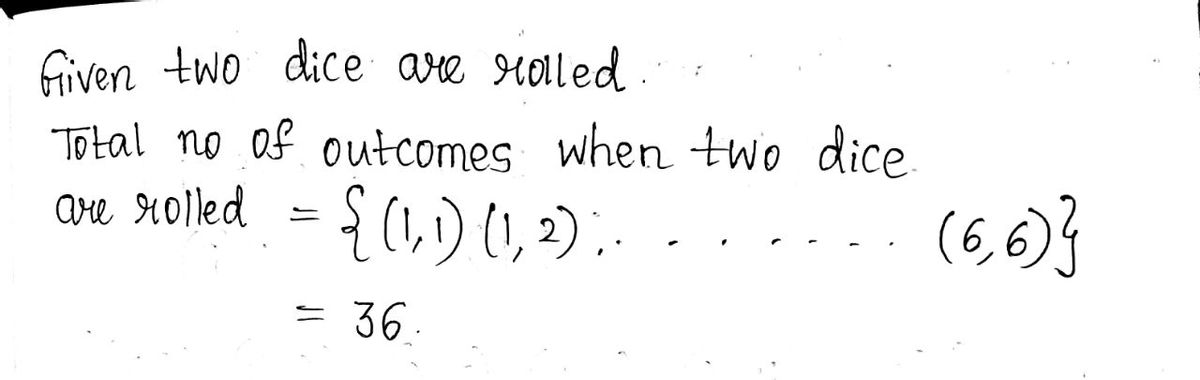
Step by step
Solved in 3 steps with 4 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
