Two blocks, each of mass m = 3.80 kg, are connected by a massless rope and start sliding down a slope of incline 0 = 27.0° at t = 0.000 s. The slope's top portion is a rough surface whose coefficient of kinetic friction is pa = 0.180. At a distanced = 1.80 m from block A's initial position the slope becomes frictionless. (Figure 1)What is the velocity of the blocks when block A reaches this frictional transition point? Assume that the blocks' width is negligible. %3D
Two blocks, each of mass m = 3.80 kg, are connected by a massless rope and start sliding down a slope of incline 0 = 27.0° at t = 0.000 s. The slope's top portion is a rough surface whose coefficient of kinetic friction is pa = 0.180. At a distanced = 1.80 m from block A's initial position the slope becomes frictionless. (Figure 1)What is the velocity of the blocks when block A reaches this frictional transition point? Assume that the blocks' width is negligible. %3D
Related questions
Question
need help with this review

Transcribed Image Text:Learning Goal:
To apply the principle of linear impulse and momentum to a system of
particles.
I Review
Integrating the equation of motion, as applied to all particles in a system,
yields
Part A
Σm (vi) + ΣΗ F, α = Σ m (v),.
Two blocks, each of mass m = 3.80 kg , are connected by a massless rope and start sliding down a slope of incline 0 = 27.0 ° at t = 0.000 s. The slope's top portion is a rough
surface whose coefficient of kinetic friction is p4 = 0.180. At a distance d = 1.80 m from block A's initial position the slope becomes frictionless. (Figure 1)What is the velocity of the
blocks when block A reaches this frictional transition point? Assume that the blocks' width is negligible.
where m; is the ith particle's mass, V; is the ith particle's velocity, and
F; is the external force that acts on the ith particle. This relationship
states that the sum of the initial linear momenta, at time ti, and the
impulses of all the external forces acting between times t, and t, is
equal to the sum of the linear momenta of the system, at time t,. If the
system has a mass center, G, the expression becomes
Express your answer numerically in meters per second to four significant figures.
• View Available Hint(s)
m(vc)1 +Ef F; dt = m(vc)2
It vec
?
This expression allows the principle of linear impulse and momentum to
be applied to a system of particles that is represented as a single
particle.
v = 4.6
m/s
Figure
< 1 of 1
Submit
L.
y
Part B Complete previous part(s)
Part C Complete previous part(s)
B
-d-
Provide Feedback
Next >
Expert Solution
Step 1
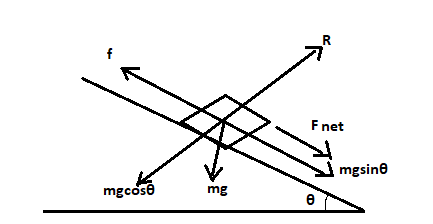
Given values:
Mass of the block,
Angle of inclination,
Coefficient of friction,
The distance of frictional surface,
Diagram:
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images
